Newton's invention of calculus: What is Newton's calculus?
Hello, welcome to my talk, on Newton's invention of calculus. In here I will talk about what is exactly the Newton's calculus? Principally, calculus is an evolving thing, and as early as in the ancient Greece, Archimedes had used the method, very similar to the calculus to obtain the volume of a sphere, but why we say today Newton is one of the co-inventors of calculus (with Leibniz). This talk would make an explanation on this. In this talk I will introduce: -what is the Newton's calculus? a brief introduction will be made on this; - and then I will introduce three Newton's quadrature rules, which allow calculus for more complicated and practical applications; - the proof of the quadrature Rule 1, we will see how Newton solved the complicated calculus problem; - and then the application of Newton's binomial series, which simplifies the complicated problem for calculus; - and the summary of Newton's calculus, on what problem Newton solved or what breakthroughs Newton had made for calculus.
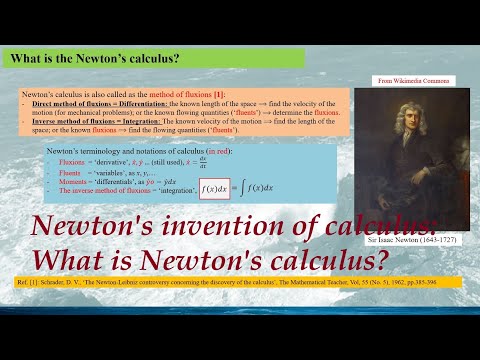
Isaac Newton was one of the greatest mathematicians in the history, and one of his greatest contributions was the co-invention of calculus, but what is exactly the Newton's calculus? Here I would like to make a brief introduce on that. Newton's calculus. is also called as the method of fluxions, based on the reference [1] here. For Newton's calculus (as the modern calculus), we have two different ways: - the direct method of fluxions, it is equivalent to the differentiation of modern calculus. For instance, for the known length of space to find the velocity of the motion for mechanical problems, or the known flowing quantities, Newton used the word 'fluents', to determine the fluxions; - and the inverse method of fluxions, which is equivalent to the modern calculus, the integration. For instance, if the velocity of the motion is known, to find the length of the space, or if the fluxions are known, and find the flowing quantities, the fluents. In Newton's calculus. Newton's terminology and notations for calculus: - Fluxions, equivalent to derivative, Newton used x-dot, y-dot..., these
are still used in modern calculus, here x-dot is the differentiation of x with regard to a variable t. - Fluents are the variables, as x, y and etc; - Moments the differentials. In Newton's notation, it would be given as y-dot*o and the modern calculus would be given y-dot*dx; - and the inverse method of fluxions, the integration. In Newton's notation is given
in a rectangular box, and now the integration is given as this, the Leibniz notation. Principally, Newton's calculus is a combination of his important developments in mathematics, these including: - the binomial series; - the inverting algorithm; - the quadrature rules, these are the topic in this talk, and we can see the obvious calculus elements in these rules. In the next few slides, the quadrature rules will be introduced. In this slide quadrature rule No.1: the quadrature of a simple curve: if y is given as the simple function of x, its curve AD, where a is a constant, and m and n are positive integers, then the area of the region ABD is given as this expression, based on the reference here. In modern calculus, this rule is very simple. however in Newton's time, this development is very important. Next we will see two examples. The first example is we have a function y =a*x^2, this is an elementary power function of x, we can easily calculate y with an increment Delta_y, because the x is increased by Delta_x, so we can calculate the increment as this, so delta_y would be given as this, and then we can calculate the derivative or the change of y with regard to x, so it is given as the limit of the ratio delta_y over delta_x, when delta_x is close to 0.
so we have the expression for the derivative as this, and this, because Delta_x would be close to 0, so the second term can be dropped. Obviously such elementary expression with the power function of positive integers must have been available in Newton's time, and the one of the Newton's contributions was to extend the calculus for the more complicated functions, that is, the power functions of fractions. If we look at the expression here, we can see obviously Newton has extended the theory to the power function of fractions, here m and n can be any integer, but m is not equal to -n. For instance, suppose we have a function equaling to a*x^(1/2), this is a special example of the expression y =a*x^(m/n), with m =1 and n = 2. How its derivative and integral can be calculated? Newton gave the answer for this in this quadrature rule. Here we must be noted: - before Newton, there was no method for expanding the function as a (x+ delta x)^(1/2); - and it was Newton who made the breakthroughs in this, based on his binomial series, such an advancement allows calculus for much wider applications for practical problems; - From the modern calculus, we can easily see the quadrature rule No.1 is correct.
Quadrature Rule No. 2, the quadrature of curves compounded with simple ones, that is, if the value of y is made up of several such terms: simple curves, the area should be made up of the area which result from every one of the terms. This rule means if we have a function as y = y1 +y2 + y3+..., here y1, y2 and y3 being the simple curves, as we seen in the previous rule, thus the modern expression of this rule is given as the integral of y is the integral of y1 + the integral of y2 and + the integral of y3, and so on. This can be easily proved to use a graphic way. For example, if we have the area for a function y1, this is the hatched area, so the area is calculated as this integral, and we have the second area given as this, the integral of y2, given by this. Here we make the difference of these two areas, so it can be easily seen graphically how we can do this. If we use the area
of this, take away as this, so we have the hatched area as this, and this area can be calculated use this expression, the integration here. Therefore, we can prove the summation rule of quadrature given as this. It should be noted here whether the rule is for summation or for difference, the principle is exactly same. This is the proof of the quadrature rule No.2. The quadrature rule No.3 is for the quadrature of all other curves: if the value of y or any of its term be more complicated, and then they must be reduced to more simple terms, and then use the rule No.1 and No. 2,
we can obtain the area of the complicated curve. Based on the Newton's binomial series. This is the only expansion Newton used, we have seen this before, and here each of A, B, C, D... represents the previous term. And now we may use Taylor series instead, however it (Taylor series) was not available to Newton: Taylor series was developed after calculus.
Take an example, P = 1 and Q = -x^2, m = -1 and n = 2, and based on the Newton's binomial series, we can expand the binomial function as this into the binomial series this, so from this binomial series, we can see each term of the binomial series is the simple curve of the power function, and the area corresponding to each term can be easily calculated, so based on the Newton's quadrature rules, we can obtain the area of the complicated function, as well as the derivative of the complicated function. This is the purpose Newton developed his quadrature rules for calculus. In the next few slides, the proof of the quadrature Rule 1 will be made, and we will see how Newton solved the complicated problems. It is interesting to see Newton used an unusual way to prove the quadrature rule: he actually started from the known area of a curve or the quadrature: z given by this, and then he derived the function for the curve. here suppose the area of ABD is taken as
z= z(x), see the hatched area. Now he supposed the point Beta on the x-axis, with a small distance, Newton used 'o' to represent the small distance, Beta to B. hence A-Beta would have a length x + o, and z(x + o) would be the area: A-Beta-Delta. Newton then introduced a rectangle B-Beta-H-K of a height of v = BK and Beta-H, and the area of the rectangle is the same as the area B-Beta-Delta-D beneath the curve in this small region, as such, the area of B-Beta-Delta-D would be simply calculated as o*v. In Newton's proof of this quadrature rule, he assumed the area under the curve is known, given as z(x) expressed as this; and his purpose was to find the instantaneous rate of change of z, as y is the derivative of z with regard to x, that is, to find the function of the curve y. It should be noted, even in Newton's time, it is well known that the derivative and the integral calculations would be an inverse calculation. This means if we find one, for example, the derivative or the integral,
then we can easily obtain the other, simply use the inverse calculation. Following the Newton's derivation, we can take c as the expression as this, and p = m + n, so z(x) can be expressed as c*x^(p/n) if we see this expression here. so we can obtain the equation as this, so z(x)^n = c^n*x^p, and if we consider the increment of the area due to the increment in x, so we have the expression as this, and as we have seen before: the area of z for (x + o), it should be expressed as (z + ov), so we have the expression as this. Next Newton applied his binomial series for the binomial functions, this and this part, on both sides. so we have the expansion for the binomial series here, the left-hand-side given as this, and this for the right-hand-side, so consider the original expression here, so we can take these two terms away, thus we can divide the equation with the small increment 'o', so the equation would be given as this, here in this term, there's no 'o' and this one there's no 'o', and this term with one 'o' and this term, you can see here: 'o' here and 'o' here. So if we take the limit of the equation when 'o' is close to zero, in such a case, v would be equivalent to y, hence we have the expression, reduced to this, and we can obtain y given in this from this equation, so we replace back of the z function, c and p, so we have the expression for y as this, and this, and this, and then we can see this part would become as this, and here the power (-1) is (this), divided by x, and here (-1) would become this, divided by x^(m+n)/n. Now we can cancel all these same values
for the numerator and denominator, so here n would be cancel out, and (m + n) would be cancelled out, and this term would be cancelled out, therefore, we have the expression for y given as this: a/x, (and the) denominator would be 1 divided by x^(m+n)/n, this will give an expression for y simply as this, hence we finish the proof of the quadrature rule No. 1. From the expression of the area of the curve z(x) here, we can derive the curve would be given as this. Infinitesimal calculus or more simply 'calculus' is basically an evolving thing: - as earlier as 250 BC, Archimedes employed the similar technologies to obtain the area of a circle and the volume of the sphere; - and many other scholars have contributed to the calculus developments, these both before and after Newton and Leibniz. Then a question would be: why we say it is Newton and Leibniz who co-invent calculus? the main reason for this is both Newton and Leibniz had made the breakthroughs, which brought the calculus to much wider practical applications. In Newton's case, his contributions include: - Newton's binomial series, for the generalised binomial function, which is a huge advancement in analytic mathematics; - the quadrature rules, especially the Rule 1, for the derivative and the integral of fraction power functions, this is another big breakthrough to bring the calculus for the practical applications; - the basic rules for decomposing the integral terms to make the application of the calculus possible for the complicated functions; - the inverting algorithm of infinite series; - some fantastic examples of the calculus applications, such as, the infinite series for sine and cosine functions; - the earliest applications of calculus to the dynamics and motions, creating a new era for physics and mechanics.
And I think without the Newton's contributions, calculus would be limited to some applications, and we will not have the fantastic mathematical tools, such as the Taylor series...
2021-02-26 19:53


