Memory, Modularity, and the Theory of Deep Learnability
And. Also what if you want to discuss. Or brainstorm, about how should we should think about it conceptually. Architectural. Ease of going forward or more complex tasks. So. Deep, learning of course has made amazing strides. On. Several. Engineering applications, on, speech recognition we, really have a below. 5% whatever, rate on image. Net data. Set we have it under sorry-sorry. Sorry-sorry that. We. Have under 5%. But. Still down several. Complex starts where we are far from perfect like true. Natural language understanding the, way we have conversations with each other or even. Logic, there's. Almost no. Good understanding, of how to put logic into declaiming. Now. Peopling. Works well, but do we really understand, why it works. You. Know what is the exact limits of deep learning do. We understand, what class of real world functions the pony can learn can we say that the type of function that we learn and, the x not, learn and, other. Means specific properties, about real world functions, that make them laudable. Using deep learning and. Note. That I'm specifically, talking about lot ability not just representation. We, all know that these networks as, long as they have non-linearity, can represent any, function. Any. Computable function here, we're talking about learnability that means given, training data set I should be able to learn it using the gradient descent, do. You care about efficiency or, no yes. I. Mean. You're not talking about just, even polynomial. Time learn about this good enough just whether it can own it or not. And. I wanna suggest that instead of just focusing on real engineering. In a sense it, is also beneficial to look at synthetic days except sex to understand this conceptually, and synthetic. Data sets means that the data the training data is obtained from some mathematical, function, and. There is a good reason to do this because, when. I take you give you a real data set and you get, some loss. Let's. Say it's correctly classify. An 80% I guess, you'll know whether it has fully learned the function to the best possible level because, you don't know what is optimal point and. Synthetic. Data sets you have this advantage and, you know what the ground truth is so. If you know that the model generating the data set is small and, you know it can be learned to zero error using, somewhat, unit. Test the how. Well this technique. Technique or any learning technique for that matter does, on synthetic, mathematical. Performance, so, here are some good possible, mathematical. Function. Classes a good, one for non linear functions is polynomials, this, is the classic one for representing, ordinary functions you, know also have decision trees grass can deep learning learn. All decision trees of of limited. Size you. Can also ask functions, that are generated using teacher. Deep networks so, you could just have a fixed. Synthetic network small. One and you can have input-output pairs from that but, you don't know the black box it's a network. Is about black box you can ask whether or not II plan again learn this and. Particularly. Interesting. Is, the. Real world functions in. Which synthetic class of these, does it fall other. Some specific properties, mathematical. Property is that these real world functions have that, is come, from one of these classes that makes, it more learners. So. That will be the first part of the talk in the second part I will make it much. More open-ended. And. We. Will get into questions like what should we up it actually what. The current deep learning framework, that Berry has is it sufficient or, are there are some major architectural, changes required to, handle more cognate complex, cognitive tasks, like natural. Language understanding or, logic and. Particularly as I will try to argue that we need some. Biggest, level changes like you have a more modular view of deep, learning and we need to have good, memory, support in addition to a deep network. So. This part will be more speculative and if type on time permits I hope we, can have a discussion or brainstorm, about what you think are the right, ways to extend this architecture and. The. Main points. Rather. Than wait is that. Here. Are some of the theoretical results okay first, from the function classes of polynomials, we will argue that we will, prove that polymers. And we learned using deep, learning then. We'll go to learning. Teacher networks will. Show, that very shallow. Teacher networks of depth, two or three especially. Depth you can probably be learnt using deep learning with, some assumptions but. Then on the other hand we will argue that the very one a very deep random networks you want to take a random teacher network and I. Make it very deep then. Somehow it's it's very hard to love those in fact they might even become cryptographically, heart Allah and I'll show evidence for that I'll, also give some evidence to show that if your network.
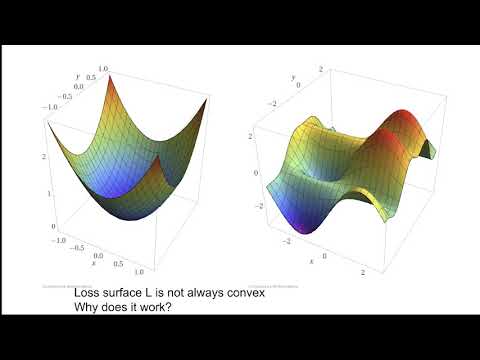
Has Some modular structure that means if you broken down into pieces which, thin connections then that actually helps it. In making more loadable and finally. We will explore, possibilities of adding memory, and modular, structure to be to. The deep learning architecture, so. When you say easy to learn are, you going to allow the learner network to have depth, somewhat more than the share then the teacher network yeah, I'm allowing it to have more I'll give you results saying. That sometimes it may not even be necessary okay. Let's. Go through the basic deep, learning framework, you, have some unknown function, and. You. Just have input-output, pairs from that function, they, will be drawn from from distribution, maybe. From from real-world situation so that you can predict its value on some new inputs that you will see in the future and. This. Is exactly like, linear. Regression, where. You have some data points are and fit a line to it but, instead of just fitting a line you want to fit a higher dimensional, curve which. Is given by a nonlinear, function and one. Way to get a, nonlinear function is to have a deep network with. A nonlinear. Activation, and, if you make this deep enough you can actually represent, any function which. Of course doesn't mean that you can learn any function. So. You are. Given input-output pairs and you train the weights of these optimally. Match the. Input-output pairs and, the way you train it usually is you. Look for a for given set of weights you check whether, it agrees with the. Function. The, training function and. Minimize say the square loss, so. This is your loss and then you take a gradient of the loss with. Parameters, keep, shifting moving the weights so, that the loss decreases and. You hope that in the end it will match. The, function it is most of the input-output, pairs now. Good, if the loss surface is convex the. Loss of its convex you guaranteed, to reach, the minimum point but. In real. World and especially in deep learning you, can it's easy to prove that the loss surfaces is not convex because there are many many minimize, and you don't know whether every minimize is equally, good as the, global window so, why does this work in engineering, applications. It. Has also been found that in. Real, networks, as you. Go up you, are learning. More and more complex, concepts. So at the very on. On image this, is an network. For analyzing images and. The very large layer you understand. Things like lines, and curves or edges then as you go off you find a complex shapes and then, at a very high level you might find things like face of a person or, a face of a cat and. It also found there's some evidence to show that the. Are the, outputs. Get sparse or as you've acquired because you're finding less, and less complex. Phenomena, in a piece, of importance. So. As I said it. Works well but. We would like to understand conceptually, why.
It Works well and when would not work well. Let. Me point was some rated work this is very limited set of energy later work so, for another non convex optimization minimizing. Non convex optimization. There. Are statistical, physicists, who have argued that the. Lost surface in for, deep learning, actually. Might have many local, minima but, most of the local minima have values very close to the global minimum and they. Arrive. At that by modeling, the loss of as some kind of a Gaussian random process. There. Is other works which explain why SG the specifically, the stochastic aspect, of the gradient is it helps, in escaping, saddle. Points so, even though saddle points for gradient descent is problematic, for stochastic, eighteen doesn't actually, it, can escape in. Terms of not ability of feature networks, there are several results which. Talk about how, why to layer teacher networks ran, your networks can be learned by two, boolean, networks. In. Terms of overall, conceptual, we have deep learning Michael. Elias has a theory that that. Deep learning the. Layers are nothing but doing dictionary learning. On top of it is an iterative Li so you go from a dictionary. Over. A big dictionary of atoms, along, the lowest level concepts and then you go down all addiction is originally, learning it high level concepts and so on so forth. Modular. Architectures. Have been proposed there's. Something called caps use which is produce by Hinton and. Recently. Papadimitriou and. Some. Of his colleagues have argued, how, in deep networks, in the frame you might have the notion of pointers something, some people's assembly pointers pointers, can point to complex changes. So. Here are some of the exact results we will go over. So. We'll start off with just. Linear. EECOM. Position just, a linear non, convex problem. Which is no right or oxidation when you're trying to express our matrix. As a product of two thin matrices and this is non convex and. It. Is proven that if you apply gradient descent on this problem to minimize the error for, Venus norm of the error then. There cannot be any bad, local minima, there, are many minimums but they're all global. This. Can be has been extended, to deep learning. Deep, linear, networks. Then. We will go to nonlinear functions we will show that polynomial can. Be learnt by using, networks. Of depth to where. The size, of the network depends, on the degree, of the polynomial, and. Then from there we will go to higher. Depth networks will show that the. Learnability of such. A teacher network actually, drops exponentially, in the depth and as. The. Height H increases this actually becomes more like a cryptographic. Hash function, we won't pull that exactly but we'll give some evidence to that effect and. Finally. We will, we. Will get into modularity. Structures. And we will argue that if the network is modular then, you can do something to it to actually make it vulnerable. Any. Questions your feet will interrupt me at any time, any. Discussion points. Vague. Ideas can you explain the footnote. Oh yes. Yeah. So. We will not assume here that the input data distribution. In these feature networks or four corners is adversarial, if you assume that that in, or, adversity or they're in fact problem is np-hard even. For learning of one layer of network okay, so we will assume a more benign distribution, specifically. Maybe a partial distribution. Well, broadly it is that you want to learn the function at. Least up to you, know 1 minus epsilon accuracy. Or, let's even even if you get 90% this F is a binary function if, and we got a litigator 90% accuracy that's you're doing um inaudible and in. Polynomial time and this, is assuming the same Gaussian, input distribution. Explanation. The DVD factory. Rocks with the viscosity, so. If. The degrees higher but this term, the smaller. What. Is exponential, in the degree the size, of the teacher of the selected, unit work cook. So. Let's start off with just simple non convex problem of linear decomposition, where. Let's say you have a Netflix Netflix, ratings. Movie of users your movies here and we. Believe that this can be, represented. By using a latent product. Of two latent matrices in matrices they say the movies belong so on topic users. Artists in certain topics and. The. Question is now if you try to recover. These by. Using gradient descent by minimizing. The difference, between these two then. When. You converge to the right you. Know the right decomposition. And this is basically usually, done by done. By using SVD, if the matrix is full, what. Can be proven is that just. Tensor, flow like gradient descent will also not. Get stuck in any local minima outside. Of this. Which. Is quite surprised was, only recently shown and. This, is can be viewed as a result, in deep learning because, this.
Product Of tomatoes is exactly a two layer Network except, that it's linear it. Is just a product of these two matrices there's no non non linearity, and. So. You're basically giving different inputs user movie ratings here and, you wanna match it based on the products. Now. This also generalizes, to deep linear network that means even if the pseudo network is linear. No. Matter what architecture it has you will not get stuck at all you. Know suboptimal. But. Linear networks can only express linear functions this is not very useful for learning real world functions. So. Let's go to learning. Polynomials, which. Is classic, way of expressing nonlinear, functions you're, just trying to learn some simple. Polynomial, function let's see let's see how a, simple function of degree do so. What we show is that a. Degree. D function polynomial. Can be learned using n to the power D, sized two layer Network where n is the number of a zeros and. In. Fact. You. Can even reduce the size of the piece ruin Network if you assume that the polynomial is sparse, that. Are that, we don't have full proof but do we have some mild, evidence for. And. The, reason why you can learn a problem is actually very simple using. A tool a language let's, think about a polynomial, of. The. Basic point is a column of degree P can. Be viewed on, any variables can be viewed as a vector. Over. N, to the power D dimensions because you get one monomial, for each as. One, of the basis vectors so you can express it as a. Vector. Over these these basis, directions so if you just have a quadratic function. There. If you just have a degree. Two function over two variables and, this is homogeneous for simplifications you, just want these three basis evidence and any polynomial can be expressed as a linear combinations, and, for simplicity if you think that the activation is quadratic then. Basically you get for. Each hidden unit you get a different, quadratic. Functions as, long as this lower layer is random, these. Are going to be fairly independent. So. As long as you get more than three of these you can prove that you, can express a linear combination any. Quadratic function as any, combination which. Means that if you keep this random are you just train these upper, layers and if it's them assume that this is a reality. It's, easy to see that you can learn any degree. To function. So. What do you say about the non-linearity.
On The top yeah I made, a simplifying assumption that it is it doesn't any else yeah, but experimental, you can see that even, if you make it a nonlinear, like you take a sine so, sine come up all right you, can learn these things Pilger, but. Learning with linearity, is actually smaller result right that you don't even need nonlinear again no noise. Well. It's stronger in that sense but view if you let alone threshold at monomials and it's because you. Want to turn the region. And. You can actually argue, that you don't need to freeze this part you can train this as well and still, you along this. So. This is okay, but if there is a two inputs where, the. Green layer can, be a linear. Function of the underlying. It'll. Be just a renaming. Of this. Under, under some yeah. Transformation. Okay okay. Hmm. But. You need to have enough capacity to represent the monomials, I guess yeah. So X alone will you have more than into the body of these you've. Got a each monomial sorry. The. Surprising thing is if. The number of Oh Nova is the possible number of monomials one hundreds but. You just have three spots things, right. It, turns out that you don't need or hundreds of nodes somehow they adapt if. You have particular try to find it out try, to learn listen. You. Know let's see ride-alongs Nagano X. X. About five plus y to the power 5. Yeah. Now. Over. Two inputs gonna have 5 choose 2 power. Possible. Things but. If you just have small number of things here it's somehow it adapts to the right monomials, so there are no cancellations, happening inside the network. Twice. Sometimes, the translation. Happening. That is one-to-one some of your only one more time. The. Right combination, so they cancel out in the right way and then. What. If the labels are approximately. A polynomial. Yeah. So we played with a random or. Randomized. When everything is right, pretty much same argument quite. Trivial if you see it's mathematically and other things will all correlations, will drink. This n doesn't change that much if you if you have a demise that, was real. Okay. So this, so. What is a dependence, so as a degree. Number. Has. To be a to the power D, but. It can also be smaller if, your problem, in the sparse normal, sparse is probably just, proportional is possibly not square does just, exactly equal disperse know I once, I, don't have a proof of how, it burns possibly I can prove that if it depends on how many key out of those n variables then you need one decays party I think. That one sort of thing but also empirical you can see that with sparse s then you which can turns out that you can only too much is. That a simple information theoretic argument, that says that. Number. Of nodes proportional. To the sparsity enough, to capture, the. Capture yeah. Representation. Should be representation should be zero. So. This is good but it's gets too wide for high degree and who represent, any complex. Function you really need a high degree that's. Why it's important. Representations. Which are deeper let's. Have. A question, from the other room yes. It's. Time flip back one, slice. So. Essentially, you're saying a, polynomial.
Function Is. A linear combination of, monomials. Yes. That's, what you're saying right exactly. Yeah, that. Doesn't need a proof. That's. The purpose of any the main idea the proof is fairly simple except. That when you can do the details of what. Happens if you change this quadratic activation, to a sigmoid. Or some, other activation, and suddenly, you start allowing the lower little bit rain, then. It does not. But. That's what now that's not what you just said quickly you said using, the base if, we, limit the base to be more, normal. And. Then, we do this simple linear, combination, then we are guaranteed. Exact. Final proof idea that is giving the main point of proof here okay. Okay. So. Let's go to 200, more complex. Nonlinear. Functions let's, go to teacher. Networks, that are deeper, yeah. So. In the student teacher framework, you have a teacher network that is a black box but it, is also a deep network and you give an input output pairs, from that and, then you are training a student network. To. Fit these input outputs and. It. Makes a lot of sense to study this framework, because, we. Often represent we, often believe that real, world functions can be represented by using a dip network so. If. You are trying to, functions, then, we better people to learn network. That is capturing. That function. So. Instead, of so, we'll just take a synthetic deep, network here let's. Take a random deep network here and let's, try to, check. If it can be learned by using a soda network lossy, value we know the shape of this network. I'm. Particularly needed with this experiment, we took a random deep network very dense step we, fix the width to be about hundred and. This. Is with value and the civil fine, activation, and we, check how much the accuracy. Drops with the depth here's the applause okay. Applause off point file means basically not learning and it was even a random prediction. Will give you an appointment, one. Means you're you're perfect so notice that is very small depth you, have a very high accuracy. So you get really learning depth to networks quite, well and, you can kind of drops progressively, as you increase the depth by, depth 14 or so you basically almost, no, know nothing about the function so. The function gets very hard to learn at, least using deep learning at. These depths. So. With these observations we, will next. Show. That we that we can theoretically prove, that for, small depths there, is a reason why you can learn with, pretty good accuracy and, we will argue, that for larger that's actually the learnability not just using deep learning but using. Exponential. And. Both are the same shape same. Shapes as we married the celo to the pelvis means very to the depth we allowed it plus or minus two we. Actually allow the width also to double, and. It. Doesn't make that much difference. So. Let's try to look at learning just teacher networks of depth to, and. See why this is easier, so, you have a teacher network with. Weights W and a swivel network will initialize with some random weights theta and. Then you're doing gradient descent on the loss and. You're hoping that theta goes starts. Approaching W it, does not fully, approach W it can force of permutations or may, or may be doesn't match fully but it matches. In the function value. And. What. We found is that there is a, conceptual, argument where. You can actually map this dynamics. Of this gradient descent to a, certain. Electrodynamics. That. Is you look at these weights. Look, at these weights W coming, into each node you can think of each W, is director each theta is the has a vector but sometimes we just assume, that these two are already the same, the.
Top. Layer are not. Different, so. Then you can write these points, these w's think of them as points in high dimensional space and you. Can think of them as fixed protons. Which. Are not move which are fixed and then you can think of the student networks hidden, weight vectors call them theta is you, can think of them as electron in space in the same direction space and as gradient descent is happening essentially, it's trying it's moving these electrons, which is the Solent Network it's, moving the electrons and hope. Is that somehow it will match up with the permutation of the protons, which, are the final desired weight vectors and. If. You track the dynamics it exactly matches this electro dynamics where there is a certain potential function where, the electrons, are getting depend according to that potential function and they're. Getting attracted to the protons chroma, depredation function and, eventually. They you want them to line up and the. Reason why maps. Matches the potential function is because if you look at the loss. You. Can write each. Function, as some, linear combustion, because, we are approximating. That assuming the top thing is linear so it is some linear combination of these, sigmoids. With. Dotted with theta is minus WS, so we expand it out you will get a pairwise term for each electron electron and, even a pairwise term for each electron proton, and. So. You will basically get, some potential function for, for, repulsion for. Electron electron minus. Potential function for electron proton and the, dynamics exactly. Match 1 to 1 now. The. Potential function depends, on the activation function. So. This is not a standard potential for assignor, potential, function in real life in, the real world in physics is 1 over R and for, this particular potential function it is known that. If you start with the percent of positive charges fixed them and you take a negative charges and they allow them to move they must actually eventually, line, up for the implementation so, it works for that but, that doesn't corresponding to correspond, to any real activation. What. We show is that there is some synthetic activation, function for, which the same property holders. And. There's, some other many other results, for two layer networks there's one result for hell you with, someone ensure that this. Should hold up and some other, assumptions. So. That does it for two. Layer networks now let's go to. Deeper. Networks. What. We will argue, is that as the network gets very deep the function gets very, hot or. Important. This is that we use quadratic curves. In. This analysis quite important I don't. Know it. Seems. A world and I'm not next one without politics. So. We, will argue, that very, deep networks might be very hard and.
Here. Is the reason it. Turns out that random deep networks are almost like random songs they. Are almost like random hash functions here's the reason, if. You take an input essentially. Each layer is performing a rotation. A random, rotation and then. It is doing some non-linearity. And doing that for a node you will argue that as you do I do, this successively the, outputs are basically no correlation with them in. Fact let us take some correlated. Inputs from very two inputs that I have a very small on you and let's study what happens to the angle as you push it to this network it. Can be sure, that the angle will, go on increasing and. Over. The over different. Layers eventually. Will become almost orthogonal you. Can theoretically prove, that, the, expected dot product gets drops exponentially, in, the depth which. Means they get completely, uncoordinated. So. Which means that if you take a bunch of correlated inputs and you. Push, it through this network eventually they're going to really random moving on collate do, you need that linearities. For that or even linear, not, in it already if you can just keep it linearity the angle change occasionally. But, the, did. Similar things with a. Short. Something, completely. Correlation, divider. Can. You argue that a random Gaussian but we did that thing called Dutch norm in the middle but but. That some kind of non-linearity, but that's, not surprising because I feel that if. You have a Gaussian random matrix, so. We have only to normalize it because already it's, already centered, if like everything is mean zero yes, so it starts, like this then. Like these two correlated, mini-batches. Sorry. Wow. Can. You hear me. So. I know, this for a fact that a random, matrix this. Is one. Small branch in apply, math if. You use iid. Gaussian. Random matrix. You, multiply to any, vector in. Being. Average is equivalent, to multiplying, that. Vector with, a, hermit. Orthogonal. Matrix. And. It's very it's trivial, to prove that concept, so here when you say random deep network. So. If each layer is an ID. Gaussian, random matrix. Then. It doesn't change you. Know there's not little denominator, D. Shankar. Was saying even if. If, there's no non-linearity. Then. This angle would not change in, me he, averaged me. For. The whole descent alright if the caution matrix is mean, zero. No. I mean like the activations. Are being centered every time yeah. But if. Analytics, is if. This is the participation, is means you know yeah and already things oh they, just be rotational, that's. A it's, a goodly just, did it empirically and, we, saw this behavior and, we thought this might be some reason to explain. Where. Your inputs also centered, already the, inputs are allowing, yeah yeah I don't. Know what happens if you have a product, of many. Normal, matrices because the spectrum I don't how it behaves, it, may not be a rotation anymore, maybe you're observing, phenomenon like that okay. But. Only with non-linearity, than becomes closer to 90 degrees eventually, and even. Uses to prove that it's, statistically. Sessile in a shtetl query framework, it's, hard to learn this problem, below. Exponentially, smaller than M, we. Don't prove guilt ography hardness although, it made possible is cryptographically hard but we can show that if you take K inputs. And. The outputs are kV independently small K for, K about routine we can prove that it would. Like crucial is that it's, true for polymer, large case that it's truly cryptographically, hard, so. This kind of indicates that a random deep network is not learn about which. Means that the natural functions will care deep they probably not random deep networks they, probably have a much more, structure to it which makes them learn about and the question the ball question is what is that struck me is there.
A Mathematical. Definition for. Natural function. No. Natural, function I just mean functions. In real forgive that we learn in real life. So. Ah so our, goal is to take much of the functions and say that roughly it belongs to this class it, has properties from these classes of mathematical functions you. Can argue, the most physical, phenomena, or describe, climb very low degrees, polynomials. Right if you look at almost all theorems, in physics. They. Involve fairly, lovely green. Flower. And, this kind of things that are there. Are high degrees about, but. Even a step function but it is a very common thing in practice it's not only I'm gonna block this community and, that is quite high degree before, I get quite a good approximation. Faster. -, till approach but like in finals we do it then as processing you know lot, one ticket logic that. Is so far from polynomial. But. The, issue is this if you look at the, typical numerical. Partial, differential, solvers, they, use, piecewise. Polynomial. Their local, a low. Order polynomial, you. Piece them together as. You go as you refine, the mesh or you get better and better accuracy so. Here when you talk about polynomial. You're only friends in the global polynomial. Yeah, I'm not supporting any piecewise stuff it, it. Was by, putting piecing, things together you can actually get very complex phenomenon, right. So. Here is one possible. Class. Of networks, that might be more learners and these, are networks which have which. Are more modular that means you. Have a deep network which is which could be very deep but, somehow there is a cotton layer in the middle where you have a sparse cut what. I mean by sparse fit is that the outputs of these are very sparse, so. Maybe the thresholds. In the in the neurons below are so high that only a few of them are finding in. This case what. We are we show, some evidence that this, each. A network can be learnt by using divide and conquer and, what I mean by divide and conquer is that you can somehow. First learn this lower layer and once you learn the lower layer you can go on the upper layer and why, is it easier to learn the lower layer if you have such sparse card you, can prove that if this the. Threshold, in the lower layer on high so that only if you have them afire then. Somehow this whole network is has. A high correlation with just, this lower network with, one layer or not so. Even, though this is very deep approximately. It is closer. To something of that is this not, exactly that, is what you doing already afterwards but since the proximity close to this one you can apply if you know how to solve T over two network. Learning, you can use that to get this one and then you can build. This one so. Maybe. If, we have maybe if our real world functions, are have, a block structure then. Maybe that is helping us stack layers upon, each other. So. Let's. Now go to the more speculative part of the talk and this. Is where I think I would. Like ideas, have you met you guys in half what. Should we do architecture, need in deep learning to, capture. More cooperatives difficult. Computer tasks like language and logic is. This. Is the current deep learning framework, enough for these things or do we need to have radically different. Ideas. And. Let me tell you what will be nice this, is our current view of deep learning as. You have a dog classifier, it, looks like this but this physical. Network. With just numbers, going through. There is no interpretability, here the, outputs are labels and, we. Have what we would really like is some kind of object oriented view of the world where the, output is not just that there is a dog present but something like you have a dog class. Object, aa class. Attributes. Like this is the breed is the size. And. We would like to see functions, here, function. Or procedural view here because in, real life when we, you. Know when we are doing logic we, think of applying, functions, and procedures and.
We, Don't see any function of procedures here and that is exactly what makes, deep learning so non so not interpretable, today. Not. Just that we would also like that. This this, is classified returns an object dog but, you'll also like to point to related events, like maybe you want to point it to the owner object, who owns dogs or some, other events, like you ran to a dog part and then who made the dog before so we're almost like to arrange these. Findings. Into, some kind of a nice. Baggage. Car. So. How do we bridge from this physical. View of the deep network to a conceptual, view just. Like that a functional. View object. Or interview. And. I think that was very useful for doing advanced, cognitive. Tasks. Another. Very, important thing I, think that they want is memory. So, we. Make. Use of memory so, so. Strongly in our inaudible computations. And predictions, and. The. Basic question here is when. I have a complex input or complex video or um press interaction, how do I represent. That in many and how do I store it in memory how do I link up these related events in memory. So. If you just close your eyes now. You. Can, even imagine the see of this room that. Means whatever representation. Here you have in your memory for this room it's. Actually. Reversible, that means can reconstruct that you can probably say that this is a table here there, are people here this is roughly the number of people you may not be able to reconsider exactly, but. To. Some extent, and that, that construction is. Also fades. Away gracefully in the sense that how. To ask you tomorrow what, was there what is there in this room you. Might not build you constructed, with the same level of accuracy but you'll be able to be constructed approximately, so. Even if you stare down bits in your sketch, representation. Of this object, you. Know it it gracefully, degree. Degrades. And. Also. How does this memory interact with. The actual computation of influence, on things and. I think memory probably, also goes well with this model and that means you. You, don't want to have just this one black box into a network but. You probably learn, tasks, over, time so you learnt simpler tasks with me in learning a language you, learn very simple phrases and. You pay the body perhaps, you know the module and tighten it for for learning simple rules and then you learn complex interactions, between the peers and then. Over time you learn the fine niceties of that language so, I believe that and. I would like to get your opinion whether. You, think it's the right direction to go from this end to end fixed. Architecture to. Something where you are growing a class of functions start building on top of each other and, interacting with the sketch memory. And. One. Advantage of this module is that these modules could be returning not just class. What. Is the label but also tributes, like I found a dog and the other activities of the dog. So. You should think of these modules as a function that returns a class that's object further. The modules may be heterogeneous today. We just have done, so. On single module that is learned and joined by deep learning. Modules. Some of them are based on logic they, are done by using, predicate, logic and proof, resolution. Refutation. So. We. Don't have to have just one you. Could have some discrete algorithms you could have some other optimization, framework you. Could have here my rhythms so different modules could use different algorithms, and. For, the modules may evolve over time so you may add new modules as you learn a new concept tomorrow. You find that I'm learning this new I'm. Seeing these new things and, I find that some commonality across them circle allocate a new module and then, learn it over time using the best possible algorithm. So here. Is one proposal, for how to represent complex phenomena, and, how, to store it in memory so, let's say we are just having this meeting in. The end of in the end I want to say that there is some representation, of sketch of the speeding that, means so in our minds. So. For, that I will assume that the network is modular, yeah. I'm, not telling you how we take place networks and make the modular but. I'm just assuming that the, network already has some number of modules like, maybe to detect a human we.
Have The lowest layer we have module to detect edges. And. Curves colored, in the upper layer which, take these inputs and, it acts basic shapes and, then you have components. Like eyes nose, and, then. We have computed. It a human head actually. A human. We. Like and also detect animals. So. Assume. That you have such a model network and such. Architectures. Have been proposed as I said by other people as well. But. The question is even if you have such modular networks and, you have a complex input here let's say the image of a human how would you store, that human of. That image in your memory you probably don't want to store that Robert. Not because the Robert Bob has no information for, it's useful and patientís and it's also very big so. That's what you want to do is we just want to give. That complex input and. Feed. It to the network and, see what is coming out of that input what, are the main findings and if you want to store the summary of those findings, so. We want a sketch, of that input, like is this meeting one final scheduled meeting which. Tells. You the essential, essential. Attributes, of this of this object and. It. Should be such that you can it should be loved somewhat reversible that means if I give you the sketch of that object from there you should build approximately, you can start at least the main at main, components, of that input so it, should be also, be indexable so that tomorrow. If I there, is another meeting with a related topic it, is a mall similar. To this place knitting and you can point to it and it related objects so, it should be smell smell, a deep reservation. So. The sketch mechanism, we propose is recursive. And. I say recursive, because when. You store a person you probably say that yes, face, this. Kind of dress in, this kind of and what, is the face of face itself has these kind of eyes so it's recursive we can go drill on fine, finer details, so. The. Sketch eventually. So, these modules, are putting certain. Big objects, and let's say these outputs can have, active resources, so, you want to essentially, summarize. This this computation, recursively. So that you know roughly huh roughly. What. The, input was and how it came to be this output, so. Even if there are lots and lots of modules in your network but, only a few of them fire then. A small, sketch can be used to keep, essential. Combination. Of all these files and the, main technique. We will use is basically, random, subspace and bearings using, random rotations, here's. The basic idea okay you. Want to essentially, encode the outputs, of all these modules together, when. You sketch. The final, human that you saw you and how, do you do that you just use, a simple linear, combination, let's. Assume for a moment that all these modules, are not construct, or not arranged in a hierarchy but they are always flat so, you have a network, you have just a collection of modules one, layer and only a few of them are firing let's see so, however do you sketch the output of these few modules in.
A Way so that given the sketch I can tell exactly what, are the what, are the organs what are the inputs so. This, is the simple subspace, embedding you keep, random. Rotation matrix, for each module and, you, take the output of each module and only. A few of these outputs are nonzero most, of them are 0 they, just take this later combination just rotate each module. Output for a given matrix add them up and, that. Is your final sketch and. I. Claim, that this final sketch is. A very good. Representation. Of the of the modules which fired and their outputs because, if the number of modules which fired is small and the sparsity is small enough then. By using dictionary, learning techniques you can actually tell. Exactly, which module file and what the values input binding them as long as the total sparsity, of these X's here is, less than the dimensionality of the sketch. Any. Questions, so. Here the random, random. The rotation. Fix our I was. The definition, of our I yeah. It's just a random let's, say it's just a random motion matrix. So. Think. Of X eyes are sparse, if. I'm also excited of 0 and, whichever exercise a nonzero they are also sparse, so. I, claim. That you are basically embedding, each. X I in some direction so are I represents, a rotation so you are taking let's, say this is a kind of modules you're taking a tiger and putting it in the tiger direction and. They're taking a table module filling in the table direction, so, when he was the final sketch all you need to do is look at the table, Direction the tiger direction and see, what is the value there and you will tell you understand that there's a tiger in this image for, the table in this image it's, a convenient, way of packaging. Your information, and the type information into your, final sketch. We. Require an ear of economy only full of the world, so. I can see the sparse coding connection, what's the disparate lending connection here yeah so I'll tell you that here so. Dictionary. Learning is the case when. Each RI is just 0, or 1 it is a scalar so. If. I take a sparse, company. Then. And. I take many such sketches then. It's actually learning because he's exercise of atoms and you take different a combination of these so. In that case if, it is a conditional mean this is basically a generalization of extreme learning to. Encoding, vectors and sockets. And. So. This is saying. That the outputs, are the modules or, the dictionaries, are you a minister the, outputs are vectors and these are eyes orbits so. Our eyes are 0 1 and. No. Wait. Excise. Armpits and our, eyes are suspected of. A. Disease but this is always vectors and. If only a few of the modules are firing no, digas pass combination, of vectors and that's exaggeration, if you have many such spots for many things well, if. I give you many such, sketches. Or, I. Don't even need to know these these. Vectors, X these, are these are. Vectors, and I. Can still recover them by the dictionary bus. Can. You recover them if there, is there a upper. Bound on the number of non-zeros in. Yes. You've been devoured only if the, spot. If the dimensionality, of while is. More than the total sparsity, of all the excess, information. You. Need one sketch or many sketches, no you have one sketch whose total number of flips is more. Than the essential, number of attributes in the total models. Are funding. The. Lots of a good version of this where. If you wave things differently, then you will not be able to recover those ones which I've lowered but, any one which has high enough weight so that it waits x, number. Of bits in it is. That. Weight that, proportion, of of, this sketch if, there's enough spec, if a city that wouldn't go to this one then you can get it so you can get the top elements again the top weighted, model. Firings. So. You're, stirring all the RS. They. Actually wait that's a good wish so these capital, R eyes are fixed and random, there. Are two possible statements you can make one is if you know these are eyes then. If you're given Y, I can, tell exactly which excited yeah okay that is just pasta company yeah but in fact is another shape and you can make that evil who don't know these are eyes but you have lots of such Y eyes over. Different firing for different modules you don't even need to know the are eyes you can apply dictionary learning to figure.
Out Which are these rotation matrices and then. Just. Becomes the whole framework so. You could recover both our eyes and access if you have lots of with many twice, yeah, there, you can actually recover their modules. So. This is one this is for one layer of modules only one layer if you have a hierarchy, then, you can actually the, small twist of this where you make a recursive so. When you take the. Vector encoding. Of a module you don't just take the output of that module but, you also add is some linear sum with somewhere you are the inputs all that much so. That way that thing input is successful so, once you make it recursive, then not only can you over, if you see many such vectors properly can you recover the. Modules. Of matrices, but you also check how the modules are connected to each other. Because. As yet there. Is there, is no, non-linearity. In this case, no. This is just this, is not affecting, the, forward. Computation the power computation is going on as before in. The in the. In. The metal deep network is still commuting us before we are just annotating, pending some sketches this, is just the flow of the sketches and it. Is what will store in the sketch. And. If you combine them in some fashion. It. Could be but I'm not. Really this is not really doing anything to the network. Computation reading it's just read something on the side i. If. You have some, presentation. Of intermediate, activations. You. Could think of, recovering. Our, intermediate. Depth by your earlier, result and, getting, the entire depth. So. Once you make it recursive. You. Can recover some, of. The you, know parent-child, module connections, and if. You have enough things you can actually recover the whole networks, and. Another, about is the load is you are encoding, the type type information in the direction which means you, don't have to have this complex, protocols as, to how class, structures are encoded you don't need to have this you know so many bytes for in. So many bytes for this which is what you use an object-oriented programming, construct, language and stuff so, this gives you a protocol independent way of packing types and communication, across modules. So. Finally it gives you a sketch for complex. Objects, luckily given for this meeting once, you have a module that finds meeting by going recursively, through, that computation, and sketching it you can have a short representation, for this first meeting and. That, short representation, might not be enough to reconstruct. The whole meeting it, might give you the high level attributes, furthermore. If you have sketches for the lower level, phenomena. Then they could point to the slower nodes edges so having, a hierarchy of sketches that we could who, could be useful to getting than our meeting. Leaders so. This finally get a sketch, representation. For complex objects like let's say you, solve person you have a sketched representation, for that if another person maybe all the people have are pretty, much very close to each other or in the same subspace.
You. Can have sketches for topics of discussion, maybe you have a meeting with the person X or a topic Y. So this thing will be very close to both it'll. Have similarity, with both the containing, person X, and the containing topic Y you. Could have a topics. For you gotta have sketches, for animals. Furniture. Words another, important thing is that. This. Could be useful for finding new. Concepts. Like let's say you see an animal that's, in some person is not seen a tiger at all before and, he sees a few diapers so. The tiger will have some sketch representation, in terms of the outputs of the lower much like maybe this is the I type body, type shape etc and, we'll create a new sketch vector in some, direction and as, if you see few Tigers you will see that they all kind of clustered, they form a small sub cluster in animal, substrates so, that would inform that person, that maybe, it's time to learn a new concept so, I so you'll allocate a new module and, Mabel to begin with you will allocate a very simple module you just do a simple say, editing the ball around the center is, a tiger or a simple hyperplane separating, that cluster, is a is, a tiger and over time you can learn a deep module for that class for the tiger which means that you'll start learning very fine features over, so. This is how you could potentially if. All we are your, library, of modules and. This. Could lead to so. This would lead to a whole sketch, repository, of collection of sketches which, implicitly forms a knowledge graph along. With the modular. Networking. With this one so. Knowledge graph is implicit why because our, sketch, mechanism. Guarantees that two objects, are layered then we have yeah, well similar they have a quite, high correlation so, this meeting will have a high correlation with. The topic of the meeting or the people in what in the meeting. Is. Implicit knowledge graph and. It. Could be used for retrieving later, of dealing. With some objects of object here we could see, from the sketch memory similar object, category and set it up some upstream module I.
Have. A question yes. Choose. Size by. So. Here you're saying the cluster. Subspace, they're, sort, of equivalent concept. In this sketch. Idea. Yeah. I'm losing the world clusters a little. Fuzzy Lee I'm saying, either really, think things could all be a small cluster maybe. They are all in this one subspace, and. The, South face you're talking about is, that the subspace, spanned, by the vector, of X I. Yeah. You can think of it as the rotation matrix are multiple of X I. You. Know if X, is parts then this will all lie in some subspace. If. The matrix. R I is M, by n right. Actually so think of it the case when X I has. Only. The top few bits as nonzero on the remaining bits are 0 in, that case effectively already comes a factor so. If. It sparse in that way like if, it's FX is passed in a way where only, photon entries are nonzero right. Okay. Then but, a you some space dimension, is limited, by the size of matrix RI if. Yes M by n dimensions, n is fixed. Yeah. You can at least grab squeezed. So much into, that dimension. N. Yes. Yes but, if. So. The if x i's have a smaller dimension than n, then. The. R will define some subspace, where, R. Times X is present so all furnitures, will line some subspace all Tigers, will line some subspace. Here. Are some of, Robel. Properties, that can theoretically prove. So. We were talking about learnability in the first half and what. We can prove is if is you have a modular network now. The, model that network is deep and there's. No guarantee that you take a deep network it can be learned as. A teacher network but, we prove that if you take inputs. Output, pairs and you augment the sketch. Along. With output label then. Suddenly. The network becomes much, more than a pool that's not under some bizarre. Not random networks are still random no not a, done specific reason for this because a sketch essentially, is, not just telling you the output but it is telling you the rough filter of pathways by. Which you want output it not so than that pathway but some contention, of it so. Over many, different computations. You can get, sort of the connection between the modules, if. You learn to, sketch. To mean and change you have to change them, well. I don't know how you would do it in real life right so if I learn tomorrow that there's a tie I saw Tiger tomorrow maybe. When I learned there is a tiger I revisit, all things, in my sketch memory which were related to that and you, correct them say yeah now I realize that those old things also diagram so in the conus cache memory you rewrite, then using, the new sketch, model outputs you read the address cache. Also. Makes it more interpretable, as I said because you show how the label, comes out it, has gracefully, ratio, because. If, you are applying this random rotation the subspace embedding even, if I drop some of the bits there's. Enough bits that I can recover to things at least the high level things and. Even. If there, are too many things being back into that sketch you. May not get the whole, the entire all. The attributes of the all the different of words but you might get the high level ones they should not violate once you, can also prove that you can get simple such aspects like if you have a sketch of a room with some number of people you can get roughly how many people are there what does the mean mean. Properties. Of these people. It. Is similarity preserving as I said which, gives us knowledge graph. It. Gives type, information and high level object-oriented, information, in, the protocol independent fashion without having those agreeing, upon a compiler, interpretation. It. Can be used to access pointers, because if, a sketch is talking to many things. Even. Though you cannot recover all the things you could use this as a reference and you can index into a more detailed sketch, it. Helps you in clusters, another. Thing I want to point out is floating modules so far modules were hardwired in a specific architecture, but, it is useful to think about floating, modules, which are not necessarily tied to any, incoming. Modules, but they are more like generic functions and procedures and here, are some examples of floating module think about a counting unit okay. This. Is just stomping repetitions. In an image you can also have counting of how. Many times you appear. The sound or, just more high-level around I'm thinking about something and something happened three times now.
I Want to apply, the grounding in it there this, is a unit that could be applied at very different levels of abstraction it helps to make this floating. Position you, have a clustering unit requesting. Images sounds, available. Thoughts how. Curve analyzer where, you're just given a visual curve and you're trying to capture the, curve using a few coefficients, of a polynomial or, Fourier, coefficients, but this is not just for describing. Curves on a whiteboard. But also for curve is about how, some, you. Know how some sound is changing, or, perhaps this is representing, this, is taking a sketch of presentation, of, often. Of a video sitting in frame by frame and, this. Already the. Sketch can actually take of image, and put it on the point so as the video, is evolving in age actually gives up curve in a high dimensional space so such, a thing but up line, at a very high level much. Higher levels of abstraction argue. Why this curve. Representation, is curved analyzer is potentially, a very, very. Useful component. For complex cognitive, tasks, think, about a video of a person walking or snake. Slithering on the ground or a butterfly flaps flipping everything's yeah, how. Do we recognize. That this is a person walking this is the snakes moving this is a butterfly. So, yeah there's a video we are looking at it this image is frame by frame and each. Frame will give you so, notice a good with this video is periodic well if we just to focus on this person, walking in this keep moving it's less you're tracking bias the, person's will just keep shaking. It's this and this lots of idiotic if you followed, black guys these are periodic videos the sketching, of each image will produce a point in sketch space and. The. Video is periodic so to loop produce the loop in sketches so this is one loop in the sketch space this, is in another loop I don't have a high this, is mostly in the butterflies subspace the, person software this is the snake subspace so, essentially, to tell, that this is the video of a person walking you just need to figure out what. Is this loop representing, so if you have a curves classifier, which, could take that loop and tell. You that the other coefficients or the loop and this is roughly the rotational move then, a good classifier, could actually tell you that this is exactly a person walking the, snakes of the ring and that's why if you think about this in a modular way with. Sketch representation, organizer with loading modules it will be quite the nation. Ah it, could also be applied to language - and we'd see a video of complex video can. We try to use language what. Did you see in the video that you saw a dog running jumping. Or French again, this case just occurred in a sketch space so, language perhaps one. View that one view is that parts. Of language are trying to express a way complex curved and and, express that in words so. Think about just you, know ball moving in space a ball moving in space if. It's continuously moving you can just describe using the positions but, if it's bouncing around you wanna say something okay now it bounced with this angle, and, now it's having, say bouncing back and forth so you're going to say that is iteratively, be having this periodic coil so, the moment you get into this. Expressing. Things it already becomes rich. Structures, of language so. As to conclude you know I would love to discuss. And you know what you guys think are the best ways to conceptually. Start. Thinking. About these complex already does, is. Do, you need to architectural. Changes to deepening framework and. Here are the references, you. Can go - go / - yeah.
2019-04-26 07:38
hehe! Everyone BELIEVES Google is working on machine intelligence. People think it's the complexity of an expanding world which longs to be managed cost effectively, that drives the Google tunneling effect. No... their machines are a learning vessel, being developed to merely to serve the end cause of the domination of an elite, over the bulk global humanity. Think of machine intelligence as a set of LEGO blocks, first you prototype with the toys, then you build the real deal.
The Indian fella talks like speedy gonzalez from outer space. My 'hearing algorithm ' can't do. Do you have a downloadable transcript? Thanks.
Sorry, I was trying to rush through the amount of material in an hour. It might help to go to settings (the wheel icon at the bottom right of the video frame) and set the speed at say 0.75.
There was a lot of sniffing, snorting, throat clearing and other assorted phlegm gathering sounds. I'm glad I didn't listen to this on headphones.
nagualdesign I couldn’t listen to this anymore after reading this comment
@Rina Panigrahy Cool! Manageable now...danke schon!



Transcript please. Thank you for your telomers and your mpu cycles :^ )