Fault Attacks & Side Channels
- [Guillaume] Welcome to the session this afternoon. I'm Guillaume Barbu and I will present a joint work with my colleague Christophe Giraud from the Cryptography and Security Lab of IDEMIA, which is titled All Shall FA-LLL: Breaking CT-RSA 2022 and CHES 2022 Infective Countermeasures with Lattice-based Fault Attacks. So this talk will be about fault attacks. So a fault attack is a perturbation of the processing device during the execution of an algorithm. So in cryptography what we would do is to use the faulty output to try to break the algorithm. So basically a fault attack is like when someone is trying to count 1, 2, 3, 4, 5, the people in the room and other people are yelling random numbers and then the count is incorrect and you have to do it again to double check you haven't been faulted.
So this is a well-known threat in the world of embedded cryptography, so where I'm from. And there have been some fault attacks divided against RSA, DES, AES, made almost 25 years ago. This can be done on embedded cryptography because the adversary typically has the end zone the device is attacking.
So we can try to modify the power supply of the device or try to inject some faults thanks to laser pulses or electromagnetic pulses, which will result in a faulty output that can be used to recover the key. More recent development, I've shown that fault attacks can also be applied in other contexts due to bugs on hardware. For instance, like the Rowhammer effect on the DRAM cells or access to specific registers that would control the power supply of the device or the clock that is supplied to the processor at a given time, which will help to reduce the power consumption of a device like a mobile phone, also on multi-tenant devices. So to face this kind of attacks we basically have two kinds of countermeasures. The first one we call it detective. That is we will execute twice the algorithm.
So we have the encryption here, the encryption with the key K, which is performed twice. And if the two encryption give the same cipher text, then we are P and the cipher text is output to the user. And if ever one fault is injecting in one of the two encryptions, then the test at the end will fail and we will either not return any result or return a random result or take some more definitive counter security actions like destroy the device or erase the key or whatever. Another family of countermeasures is called the infective countermeasures.
Here we will simply try to modify a little bit the algorithm so that when no fault is applied, then the correct cipher text is output. But if a fault is applied somewhere in the process, then the effect of the fault will be amplified and will infect all the parts of the cipher text that would be output. So in this case, this faulty cipher text will still be released to the attacker, but the fact is that he will not be able to use it to recover the key. This is the purpose of the infective countermeasure. So last year, two infective countermeasures were proposed to secure the deterministic version of the ECDSA. So I'll just recall here how the ECDSA signature works.
So we have an input, which is the H of the message to be signed. The signature is two components R and S, which are computed as depicted here. So the only difference between the traditional ECDSA and the deterministic version of the ECDSA is that the FMO key here, K, is not generated randomly, but is obtained by using the revision function that takes as input the private key and the input and the H from the message E. Afterward we do the computation of K with the point of the elliptical of G. The component R is the X coordinate of the point mod P and the component S is obtained as follows.
As far as we know, all infective countermeasures on asymmetric crypto have been broken in the one to three years after their publication. So all these countermeasures here have been broken by the papers here and they all concern on the RSA, different versions of RSA, but all RSA. And you see me coming in this work, we will tackle the two countermeasures that have been proposed last year to protect deterministic ECDSA.
Now what would we use to perform the attack is a combination of fault attacks and lattice reduction techniques. So that was introduced last year here at CT-RSA 2022. And the authors proposed several attacks on deterministic signature schemes, so the deterministic ECDSA and the EDDSA and they use the following fault model. So fault model is like to reason on the fault effects, we need to model what would be the effect of the fault.
We have some different fault models in the literature, like I stack a value, a variable, to zero or to all one or I can flip some beats in a variable. Here the fault model that is considered is that the faulty value XI tilde will be equal to XI plus a certain error epsilon, which will be below a given bound. So they perform several fault attacks on the signature algorithm and using the faulty outputs they gather in this way, they can construct hidden number of problem instance that they will try to solve and I will come back to this on the next slide.
What is interesting here is that contrary to other fault models, this fault model allows to handle large faults and unknowns. The fault error can be random. We don't have to know really what the error would be. So coming back on the hidden number problem, we will restrict here to a certain category of hidden number problem.
That is, we consider that we are given that the L most significant bits of random multiples of a given secret alpha mod P are null, and the problem is to find alpha given this information. So that can be formalized with the following equation. So we have TI which is the random multiple of the secret alpha mod P.
And knowing that the L MSBs are zero is just saying that this value is less than P divided by two to the L. So to get rid of the mod P notation, we can say that for every TI there exists one HI, such that TI times alpha minus HI times P is less than P over two to the L. Then it is possible to solve this kind of H and P by searching for short vectors in a specific lattice that we'll see in the next slide. So we will construct the following metrics M with the P on the diagonal and on the last line we'll have the TI that we have from the relations before. And two to the minus L on the last line here. And so we know that there exist an HI that satisfies this equation.
So that means that there exists a vector V which has the following form with the minus HI here and alpha at the end, that when we multiply this vector with the matrix M, we'll get something that is short. Indeed we can see that if we multiply the vector here by M, we'll have only components that are less than P divided by two to the minus L and that will give us a good chance to have a short vector. And this short vector will be likely output by lattice reduction algorithms like LLL or BKZ. So I will talk now about the CHES 2022 infective scheme. So it was introduced in the context of a survey on attacks that have been made on a white box implementation of ECDSA.
So basically the main feature of this scheme is that the private key D is split into two additive shares, So that rings a bell with the previous presentation on ECDSA. The input E is also split into two additive shares, E1 and E2. Multiplicative blinding protects all the sensitive variables, that is we have X prime, it is noted X prime here, which is equal to UX, U is a random value, times X. And all the variables that are manipulated at different places are duplicated so that one fault on one variable does not impact the other variable. One thing that should be noted is that all the randoms that are used to do the sharing or to blind the sensitive variables are all deterministic and are derived from the message which is the only source of entropy.
Then the scheme is the following. We compute on the left hand side first, the kind of first version of the ECDSA signature with taking into account the blinding and only one share of the private key and the input E. And on the other end we do the same with taking the other share. And finally we recombine both to have the valid signature output at the end. What we observed is that if we inject a fault in the X coordinate of the point here, either when it is returned from the application or when it is loaded to perform the multiplication to compute S1, this will produce a faulty output for the first part of the signature S1, which will infect also the final signature that is written to the attacker.
And if we consider our fault model where the XR is impacted by a random additive fault, then we can rewrite the faulty signature as follows. And this can be simplified a little bit given the actual values removing the blinding and all the sharing that we have on the signature. We can see that the faulty signature as sealed is equal to S plus UK times K minus one times UR epsilon to the LD one prime. And we'll see that this allows us to give the following relation with epsilon where two to the minus S tilde minus S is known because we know the legitimate signature and we know the faulty signature and the rest of the equation will be to recover. And actually this is exactly what we want to build H and P instance.
That is we have the TI from the H and P instance that are the two to the minus L times S tilde minus S and the unknown, which is here the right hand side of the multiplication. And we know that this value is constant. If as long as we input the same message when we inject the faults, all the randoms will be the same because the input is the only source of entropy. And so we will be able to recover this value alpha one using the lattice reduction technique.
But now we only have recovered one share of the secret. But actually we can do exactly the same on the right hand side of the diagram I've shown before to recover the other share of our secret value and then rearranging the two operations. We can recover K minus one times D, which is enough to recover D, which is the private key. Now we can talk about the contra measure from CT-RSA 2022.
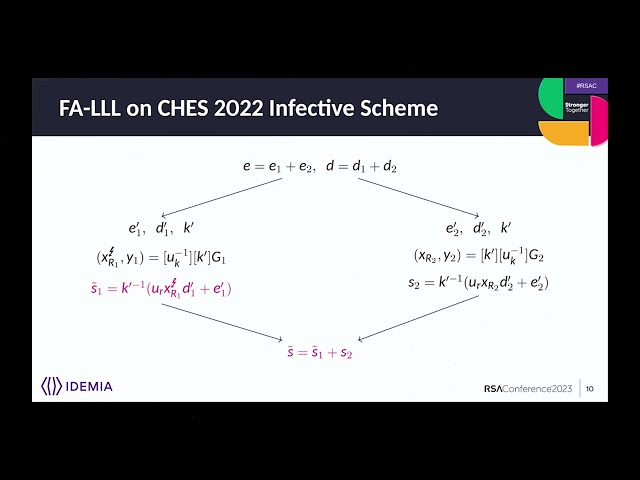
So, the ischemia is more simple. Basically all the processes are doubled and an infective factor beta is introduced, which is freshly drawn at random this time. So again, we have the same structure. We can compute two partial signatures, S1 and S2, but here the two signatures are really the same except for the infective factor, which is one pres beta on the right, on the left, sorry, and beta on the right. And then at the end we just subtract S2 from S1 to recover the original, the genuine signature S.
So we studied different ways one could use to implement this scheme. And it appeared that depending on how the infective factor is distributed on the computation of the signature, we can also perform the same attack on this scheme. So here we illustrate when the infective factor is distributed on EI and RI times DI as it offers protection on the multiplication of R times D, which can be sensitive from a side-channel attack perspective. So again, we obtain a voltage signature S tilde and by simplifying, removing all the indices on the value that are not faulted, we obtain the following relation, which can be simplified.
Noticing that all the green part comes down to position to the original signature S and again we can see that epsilon is equal to minus two to the minus L times S tilde minus S times E, which is known, times K. And we notice that it is again what we want to build a HNP instance and this time we'll be available to recover the FMR key directly by the lattice reduction technique. And with the FMR key we can recover the private key quite easily. So we performed some simulation to check the efficiency of the attack. So we drawn some random faults of different size from 64 to 250 beats and we complete six success rates over repeating the attack 1000 times.
So as we can expect all the results are quite similar for the different attack scenarios, because the H and P instance are really quite the same. Only the values are a bit different, but the nature is the same. And we can see that already with two or three faulty we managed to succeed with a low probability and with 10 to 15 faulty we can reach 100% success rate when fault are below 160 beats.
When the fault are larger, we still reached 100% success rate up to 245 beats. When the fault become bigger we have a success rate that is limited by 60 and so percent. As a conclusion, so we have introduced two new attacks on some infective countermeasures that was supposed to be secure exactly against this attack.
So it shows that the design of robust infective countermeasures is really difficult and when one proposed some counter measure, they should be proven, because we have seen that even proven countermeasures in the past have been broken quite quickly. And we emphasize also the fact that lattice-based fault attacks is quite an efficient tool as the main advantage is that it can use, it can take advantage of large faults, which is not the case when you have to consider some fault models like stockade byte or even 32 bits efforts. And that's it. Thank you for your attention. (audience clapping) - [Luke] All right, so my name is Luke Beckwith, I'm a cryptographic hardware engineer at PQSecure Technologies and I'm presenting our hardware work on CRYSTALS-Kyber and CRYSTALS-Dilithium, which is our implementation of both independent and shared modules as well as our work on side channel protection of CRYSTALS-Kyber.
So first a bit of background on the status of post quantum cryptography. So you maybe aware our current cryptographic standards are vulnerable to cryptographically relevant quantum computers. So, RSA and ECC are both on the integer factorization and elliptic curve discrete logarithm problem, both of which can be solved using Shor's algorithm on a quantum computer. So because of this, and this has actually been the process of selecting new cryptographic standards since back in 2016 for algorithms that are not vulnerable to quantum attacks.
So the first set of these standards has been selected back this past summer. They picked four algorithms as the first set of winners, CRYSTALS-Kyber, which is a encapsulation mechanism. So for exchanging keys securely between two parties and then CRYSTALS-Dilithium, Sphincs and Falcon for digital signatures. So for authenticity and integrity of messages. They're also interested in standardizing more algorithms of different cryptographic families.
So three algorithms have advanced to the fourth round, but they're all code-based algorithms. And then there is an on-ramp for new digital signature algorithms, which will be happening over this upcoming summer. And of those four Kyber and Dilithium were the primary recommendation for the public key operations. So now that we have these new set of standards and we know what the new algorithms will be, the real work of implementation and integration and seeing how this affects our current systems begins.
So, different applications have different needs for power consumption, energy consumption, resource consumption. So in this work we're presenting what we've deemed PQSHIP. So it's a flexible hardware accelerator that supports Kyber and Dilithium and can also be substantiated for multiple different security levels. So this is a hardware module that can be used to accelerate these options so they're performed more efficiently than in software. And then we also have a bit of our work on side channel protection, which I'll get into in a couple slides. So first a exceptionally brief overview of lattice-based cryptography because of time.
So both Kyber and Dilithium are based on the so-called learning with errors problem. And then right you can see a basic instantiation of one instance of that problem. So, the general idea is if you have a public value, in this case a matrix and you have a secret vector and you perform multiplication between the two and then add a small error and then release the matrix and the result, can you learn anything about the secret? And it turns out that this is a difficult problem for both classical and quantum computers to solve and fortunately can be used for both key encapsulation and digital signature schemes.
Another benefit of this is that it's easy to prioritize. You can kind of see intuitively that if you make the matrix and the vectors larger, it becomes more harder to solve. If you make them smaller it becomes easier to solve and then it gives cryptographic algorithms with this basis have reasonably high performance and we'll say acceptable key sizes. Within this family there actually are several different levels of structure. So, FrodoKEM was an unstructured lattice-based algorithm, but it had very large keys and much slower performance.
And then in the second round there was NewHope, which was a ring based algorithm, which had better performance and smaller keys. But there was concern that the higher structure might make it more vulnerable. So NIST went with the happy in-between of module learning with errors, which is what both Kyber and Dilithium are.
So this is just a very high level view of how Kyber builds the base level encryption scheme using module learning with errors. So in key generation Alice just sets up the exact learning with errors style problem. So they have a public matrix and in this case each of those entries is not just an integer, it's actually a polynomial and some ring and then they perform a learning with errors problem.
The T and a matrix serve as the public key. So then the second user can use A and T to calculate their own learning with errors style problem and encode their message inside of it. So to any observer both the seeker key and the message aren't recoverable because of the difficulty of the problem. But since Alice knows the relation between A and T, they can use their secret value to remove the effect of the matrix and the value R from Bob. And then there's just a small amount of error which can be removed during the decoding process.
So in that algorithm, and Dilithium is a similar structure, just a different approach. The main bottlenecks in hardware at least are the sampling of polynomials, because that's done using the output of a hash function and you need a large amount of data from that hash function and the polynomial arithmetic operations. So polynomial multiplication is traditionally N squared complexity, but through the use of the number theoretical transform, which is a variant of the fast Fourier transform, it can be reduced down to N log N.
But it is still itself complicated. So those are the main confrontational bottlenecks. And then of course once you start in many algorithm, you have to worry about side channel attacks. So particularly in this work we touch on the passive attacks. So, power analysis and timing attacks are the main concern.
So, timing attacks are protected against by constant time implementation. So you don't want your algorithms function to vary based on the values of the secret or else that could leak information about the secret. So fortunately these algorithms were built somewhat with timing attacks in mind. So they're very natural to implement constant time in hardware. However, the same is not true for power analysis where the power consumption of different operations depends on the secret values that you're operating on. So the basic approach that's used is the concept of masking.
So idea is you take your sensitive value and combine it with a random value and then operate on the two shares ideally independently or using specialized gadgets. So unlike previous cryptographic algorithms, Kyber and Dilithium don't have higher level structures you can take advantage of for more inexpensive masking. So this work uses domain oriented masking with Boolean and arithmetic shares, which I'll touch on on future slides. So then moving on to the methodology of our unprotected design and the flexible instantiation of performance levels that we use.
So there are four sort of high level blocks that you can split the hardware into. So you have the memory units that store intermediate values from the operation, the hashing module, which is just a instantiation of SHA-3, which is used for sampling and hashing within the algorithm. What is just generically called the format sub-module, which handles the parsing of the CM data for sampling as well as the encoding of the polynomials. And then the polynomial arithmetic module, which performs all of the multiplications and additions used in Kyber. So, there are many different applications that require different levels of performance.
So, in this work we've created a design that can be flexibly instantiated for lightweight designs that minimize area and focus on minimum power as well as mid-range designs and high performance designs. So for the lightweight design we use one butterfly unit and the butterfly unit is kind of the base operation unit of the polynomial module. And then we scale it up to two and four, which we touch on on the next slide. For the polynomial sampling all modules need a fairly high performance implementation of SHA-3 because of the large amount of data that you need for sampling.
But for the high performance design we also use a PISO, so a module that can load data out parallelly and then allow you to parse it sequentially afterwards so that you can parse one polynomial while you're preparing the hash of the next. And initially, since I mentioned Kyber and Dilithium are both module learning with errors algorithms, there is a lot of potential overlap between the designs that you can take advantage of in hardware. So, in the system, all of the modules that are shown in white are designs that at least partially share resources between Kyber and Dilithium. So for instance in SHA-3 you can just directly share 'cause it's used in both algorithms. And then for the polynomial operations you can support both.
If you just have the modular reduction needed for both algorithms, you can share the data paths and the adders and the multipliers in a straightforward manner. So then for polynomial multiplication, that's really the most complex operation within Dilithium. So for the basic operations you can just perform the operations separately on each of the coefficients without much trouble. So, addition of polynomials is just point-wise addition and the same goes for points multiplication and subtraction. The main complexity comes with the number theoretical transform. So in this case for the lightweight design we use one butterfly.
So things are nice and simple. It's a pipeline design and it writes back and forth between two RAM. So you just feed it from one RAM and right through. For the mid-range design it's similarly simple, we use two butterflies operating in parallel and then for the higher performance design it becomes a bit more complicated 'cause you start having very high needs for your BRAM throughput. So instead of processing operations in parallel in one layer, we process two layers at once using a two by two design. And then like many works we use on the fly sampling.
So, as you can imagine with those matrices and all those polynomials, there's a lot of data that you need to store in the block RAM. So by sampling polynomials immediately before they're needed, you can reduce the amount of RAM you need if instead of storing entire matrices or vectors throughout the entire operation. So then a little bit on the side channel protection of this design. So as I mentioned before, we use domain oriented masking for this implementation. So that means we split our sensitive values into two shares and then operate on them independently for linear operations.
And then use domain oriented masks, which is just a special type of and gate with random mystery fresh masks for the sensitive operations. So the goal when you're using masking is to perform operations in the domain that is linear with the most respect of their operations. So for hashing and sampling we use Boolean masking. And then for the polymer arithmetic operations we use arithmetic masking, 'cause that means that the NTT, the multiplication, the addition can all be performed linearly just on the two shares. The difficulty of this is that you have to convert back and forth between the two shares.
So, you receive inputs in the Boolean domain, sample in that domain and then you have to use Boolean's arithmetic converters, which are large and more expensive modules. And then you have to use Boolean to arithmetic converters afterwards to convert back for the final outputs. So then a little bit on the results of our implementation and comparison with other previous works.
So we compare it with a set of the highest performance and best lightweight designs at the time of publication. So, for our work we support both Kyber and Dilithium either separately or in one module with resource sharing. Our design has instantiations for lightweight, minimizing area, mid-range and high performance and all security levels and operations are supported in that one module. The highest performance implementation for us to compare against is by Dang et al, which is a implementation of only Kyber and it has separate modules for each security level. So in order to have the most strict comparison, we use the level five security implementation.
The highest performance, or the best lightweight designed by Kyber was by Xing et al. And it uses a design that has all security levels in one module but uses a client server approach. So, the client module only has encapsulation and then server has decaps and keygen.
So we compare against the server area and our figures. And then for high performance Dilithium, we compare by the design by Zhao et al, which has a similar approach of all security levels in all operations in one module. And then there was also one previous work which had combined Kyber and Dilithium and it was kind of optimizing for a compact area.
So we refer to that as mid-range and that supports all security levels and operations as well. And the platform for our comparison is Artix-7 FPGAs. So for FPGAs the area metrics are lookup tables, which are the general purpose logical elements, flip flops, which are the storage elements, and then DSPs, which are specialized elements for things like multiplication and block round, which is specialized for storing data.
So it's a specialized form of memory. The performance metric we use for comparison is the cycle count latency. And that's because while we're comparing on FPGA we target ASIC where we don't necessarily have control over the clock frequency. So for Kyber, first looking at our lightweight design and on these radar charts the general idea is that a smaller area is better, but of course if one is better in one metric but not another, it's not the literal area, but closer to the origin means fewer resources or lower latency.
So for our lightweight Kyber, that's the small blue box right there. We have the smallest area report of any implementation, which of course comes at an increase in latency. For our mid-range design we have similar area and performance to the lightweight Kyber design. So that's the orange and purple designs. But of course our module supports all operations, not just keygen and decaps. And then for high performance, the design by Dang et al has the lowest latency of all designs, but it comes with the cost of a higher amount of all hardware resources.
For Dilithium, this slide just has the performance results, because the performance of signing is significantly higher than keygen and verification. But we have comparisons with the mid-range design by Akaita et al, which is similar to the performance of our mid-range design. And then the high performance design by Zhao et al has the highest performance overall.
But as you see on the next slide, this comes at a significant increase in resource consumption. So the design by Zhao is this purple box, which has about 50% more resources than our high performance implementation. And then our lightweight design is also again, the lowest area reported in the literature so far.
And then for the combined Kyber and Dilithium, so our combined modules consume about 30% fewer resources than if you have the two algorithms instantiated separately. And compared to the other existing work on combined CRYSTALS, their design has similar performance to our mid-range design but has area closer to our high performance design and especially has a high amount of BRAM usage, though all designs require a more block RAM than Kyber because of the larger polynomial matrices in Dilithium. And then for a comparison reference with software, so we compare with and optimize assembly invitation on Cortex-M4. So for the lightweight designs, which are these lighter shade colors down at the bottom, our hardware is between 20 and 60 times faster depending on the operation.
Mid-range is 40 to 100 times faster. And then our high performance design is 70 to 300 times faster, with the outlier being Dilithium key generation. So then for the evaluation of the effectiveness of our side channel countermeasures, we use test vector leakage assessment. So the general idea is you've run a very large amount of the operation that you're measuring. So for the case of Kyber, it's the decapsulation operation is the one that uses the long term secret. So you run a large number of test vectors while collecting power traces for some test vectors that are fixed and some test vectors that are randomized.
And the idea is that if your countermeasures are effectively breaking the correlation between the secret values, then you shouldn't see any significant correlation between the fixed and the random test vectors. So for our cover design, again we evaluate the decapsulation operation. So you can see the what a TVLA looks like for a design that is leaking information in the upper right.
So, all throughout the design there is a high amount of correlation between the two types of test vectors and so there's significant leakage throughout the design. Then with our countermeasures enabled for Kyber encapsulation, you see that no leakage is measured. And the general cost of these countermeasures is about two and a half for area and two and a half for performance.
So the general idea is you can think of you're splitting your shares into two. You would think maybe you would be twice as big or twice as slow. But in the case of Kyber, because you need the additional hardware of Boolean arithmetic and arithmetic to Boolean converters, those add significant amounts of area and significant performance overhead. So, in this case we found that the overhead was about two and a half for both performance and latency.
So, in conclusion, this work has shown how Kyber and Dilithium can be efficiently implemented in hardware for many different applications and different performance and energy needs. We've also shown the first work or the most efficient work thus far on masking Kyber and we have shown how resource sharing can be used between Kyber and Dilithium to reduce the overall resources consumed. Thank you.
Are there any questions? (audience clapping) - [Audience Member] Hi, I have actually two questions. The first is you talked about in instance standardization, what they'll be using for key exchange or what's being proposed. We know in other countries, in Europe for example, BIKE and other algorithms are preferred because they don't put put such a premium on performance. Do you see similar approaches being used for hardware acceleration for those standards? And how do you see the interplay across borders? That's question number one. And question number two is how do you in practicality see this being implemented? Do you see it being integrated with OEMs or I guess how would you see it be being used in Anchor? - Yes, so for the first question, if I understand it correctly. I think hardware acceleration will play a very big role in all of the standardized algorithms.
Kyber and Dilithium actually have fairly high performance on their own in software, but a lot of these other algorithms that are less prioritized for performance would benefit a lot from hardware acceleration. And then for these algorithms, I do think they will be integrated into hardware, especially in the context of something like root of trust where you need to do verification of firmware in hardware. Having a Dilithium accelerator is very beneficial.
- [Audience Member] Okay, thanks for that description of your hardware. It was really cool. I enjoyed it.
I wanted to ask two simple questions. First one is, did you say it supports or the hardware can support all the different sizes from the NIST selections and the different levels? - [Luke] For security levels? - [Audience Member] Yeah. - [Luke] Yes, for Kyber and Dilithium, the main difference is just the sizes of the vectors and matrices. So, it's fairly straightforward to support all of them in one hardware. - [Audience Member] Okay, that's what I thought you said.
- [Luke] Yeah. - [Audience Member] And the other one is, I think, I could be misremembering, that some of these algorithms require a source of random and is the random generated within your design or is that expected that the external device supplies a source of random? - [Luke] So right now it's expected you would get randomness externally from the hardware, though it is only needed to seed the start of the operations. All the polynomials are currently per the specification sampled from the operative appear NG. So you just need the initial seed. - [Audience Member] Okay, thank you. - [Luke] Yep.
Anyone else? Okay, thank you very much. - [Audience Member] All right, thank you. (audience clapping)
2023-06-09