AI technologies for science applications inertial confinement fusion examples
And Brian Spears is the Director of the Artificial Intelligence Center of Excellence at the Lawrence Livermore National Laboratory. He's the principal architect of cognitive simulation methods, AI methods that combine high performance simulation and precision experiments with the goal of improving model predictions. He's also the deputy lead for modeling and simulation of inertial confinement fusion at NIF, the National Ignition Facility.
So thanks, Brian, for joining us and I'll give you the floor. Thanks for the nice introduction, Cristina. I appreciate it. And thanks for having me. It's a pleasure to be here. Let me make sure that I can actually successfully share my-- Yeah, please, go ahead.
--share my screen with you, and hopefully you won't have to stare at my inbox... Thousands of thousands of emails. That's right, there are thousands of them, so. Do you want to be interrupted throughout the course of the talk or should we wait for the Q&A at the end? What do you want to do? Whatever is consistent with the way that you guys have been doing it. I'd be happy to take questions along the way.
That's probably best for learning and figuring things out. OK. But if people want to wait until the end, well, I'll try to leave time for that too, so just let me know. And I think I'll be able to manage the time, but Cristina, if you could let me know when we're kind of at 30 minutes or so, that way I can try to wind down over 15 and leave questions at the end.
OK, I'll do that. If it's interactive, you're gonna be run over. Great, thanks very much. Thank you.
All right, so everybody, thank you for being here today. I appreciate you spending and spending an hour with me to talk about things. I've looked over what you've heard so far.
I know that you got a background in fusion, that you've learned some of the AI and ML tools that I'll talk about over the day. So, since I get to go in the last position I'm going to talk to you about AI technologies for science applications. The examples will draw from inertial confinement fusion. I hope the point is looking at the way we can take some of these cutting edge research tools and start putting them together into systems and actually do application. So, this might be a vision of where you might go in your career in physics, in data science, and the ways that it might evolve to actually make some change in the way that systems behave and are analyze and operate.
So, this all comes from the things that I do at Lawrence Livermore National Laboratory with a large team of folks. And essentially we're developing solutions for complex data problems across our national security missions. So we have a very big space.
There are about 7,000 people at our laboratory. We work on everything from nuclear stockpile issues to protecting our national infrastructure. There are interesting problems in biodefense and health security, detecting and preventing non-proliferation.
The centerpiece for me is fusion for energy and scientific purposes. But all of these have a central challenge. The data, both on the experimental and the simulation side, have become so rich that it is sort of an enormous weight that we are struggling to deal with. And this takes me back, actually, to a time when I was a graduate student at Berkeley. And we had a challenge to help first responders deal with people who are trapped in buildings.
And imagine the scene, a first responder comes in, there's a victim trapped under an extremely heavy pillar. You have two choices. One, you could send in some robotic device that's automated to try and remove the pillar, and that completely ignores the subject matter expertise of people who know how to handle victims in the setting. And so the solution instead was to equip that first responder with an exoskeleton. So they could go in, they could do what they know how to do as a first responder, make quick human decisions, but they're now capable of lifting that heavy beam that has trapped the person and they can bring them back to safety. So, we're in the same situation with our data, and we need something like that exoskeleton to put us as scientists back in the driver's seat and let us operate on our data.
And so the problem that I confront most, again, is inertial confinement fusion. It turns out to be a perfect test bed for our development of these tools. I won't do the very high level background, because most of you are apparently aware of fusion sciences. I will dwell on the part that's specific to laser fusion, because lots of people enter the fusion world through MFE and have a little less experience with ICF.
But the idea being we've got an epically large laser. It's a two Megajolt laser. If you pull the roof off the building there are 192 laser beams. It's about two megajoules of energy. So, it's the largest laser that the world has ever seen, maybe that the world ever will see.
And we use all of that energy to absolutely wail on this tiny target that is about the size of your thumbnail, and inside is a fusion capsule. And so we get to the conditions for fusion by creating an X-ray bath inside that hohlraum which explodes the outside of this capsule, and pretty much to scale, crushes it down to a fusing ball, which we would like to be symmetric and we would like to be inertially-confined, for as long as we can get it to be confined. And so we do, like most of you do in your experience or will do in your careers, we use incredibly sophisticated simulations together with those experiments to understand what's going on in our fusion processes. But we do something that leaves me exquisitely sad as a scientist. We have these two strengths, traditional high-performance computing, at Livermore we do it at least as well as anybody in the world. And we also have very large scale experiments, and NIF is a premier facility for doing that.
And when we confront our simulation models with the experimental data, the shortcoming is that we reduce that to scalars often. And we compare scalar, neutron yields, and ion temperatures and the asymmetry of the capsule, with that that comes out of the experiment. And when we do so, we leave our models less constrained than they could be, and leave just an enormous amount of data on the table. So what we really have needed and are offering to the laboratory are new techniques that improve our predictions in the presence of the experimental evidence. And so just like that exoskeleton that I was talking to about for the Berkeley application with the first responders, we're introducing this new pillar, this AI pillar, which is essentially the exoskeleton for us to handle our very heavy weight data. What we do is train a deep neural network on copious simulation data, so that the network understands the, if you will, the lay of the land, the general theory of the way that the physics should function.
But of course that's wrong, because our simulations, as hard as we work on them, are never perfect predictors of the actual experiment. So instead what we go back and do is retrain a part of our deep neural network on the sparse but very rich and accurate experimental data. So now we have a model that knows the best of both worlds. It understands the theoretical picture from the simulation side, but makes detailed and precise corrections for what we actually see in the experiment. And so this new machine learning pillar, this exoskeleton, allows us to deal with the weight of our data and it lets us use our full data sets to make our models much more predictive. So that's sort of the setup for how we want to go about doing this.
I think you've learned lots of the tools and techniques that we're going to put together in our toolbox to go and do this. And I want to show you over the next couple of examples, ways to go attack a physics problem and make a difference with some of these tools. So to move forward, the things we'll draw on are really threefold.
One, we want simulation, experiment, and deep learning doing together. Another challenge if we're going to do that is that we need the computational workloads to be able to develop the data for these applications. So, our tools are big enough and our data sets, our computers are capable enough that we can make millions of simulations.
But you can't hit Submit at your local computer center fast enough to support that. So you need workflows to help you steer things that are going on. And if you're going to actually explore the large parameter spaces and the rich physics of the fusion world, you need heterogeneous exascale computers in order to get this done at the scales that we're approaching. So, I'll talk to you about these three endeavors, the simulation and experiment coupled by deep learning, the computational workflows and the data generation processes that we use, and the computers and the tools that we use as the foundation for all of that.
And together, these are going to drive forward our science applications. One quick note, AI/ML as we do it in the laboratory world is a team sport. So, we need individual investigators, but this is one team that I'm fortunate enough to work with. Our teams are often 5 to 15, 20 people, nobody can do this kind of thing alone. So, one, this is my thanks to a fantastic team, and two, it's a note to you of the kinds of skills and the things that are available that are required for doing this kind of work, just something to keep in mind as you move forward. So, I know you've had some background in deep learning, so I won't belabor this point.
I just want to make sure that we have some of the vocabulary in common for the ideas that I'm going to describe later on in the talk. So, essentially all of us are using deep neural network models to map inputs to outputs. That's what they do. And so for our ICF, we can take his inputs, the size and the radius of our capsule, the brightness of the laser as a function of time, this is how we design and set up our experiments. And those get transformed into outputs that we can observe, neutron yields, ion temperatures. And we can get there in a number of ways.
We can do it by theory that tells us how to map from the inputs to the outputs. We can do it by computer simulation, by experiment, or we can do it by deep neural network. And if we do it by deep neural network, I want us to think about going from inputs, through something we call the latent space, and back the outputs. So if you look at the deep neural network on the right, we put the inputs in at the bottom of the network, we make a sequence of nonlinear transformations layer by layer until we get to the outputs. And in this last layer, the last hidden layer right before we get to the outputs, we have the latent space or the latent representation. This is the most distilled, compressed representation of my physics input that I can get that's describable and understandable to the machine learning tool.
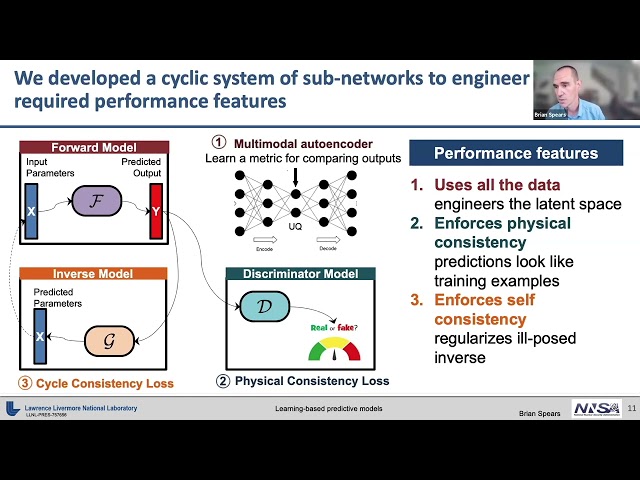
And it takes just a simple operation to transform back out into outputs that I can understand as a human. So, one of the themes that I'll talk about today is engineering and exploiting that latent space as a key strategy for capturing the correlations that are present in physical data and operating on them in a way that keeps that in the problem but then also compresses the problem and makes our life a little bit easier and faster. OK, so what do we actually do with that? Here's an example of the way we've tackled the ICF problem. We built a cyclic system of sub-networks to engineer the required performance features that we actually care about. So, one of our requirements first off is, as I said at the top, use all of the data. We're not going to leave anything on the table.
We want to take it all in. And the way we do that is by building a multimodal autoencoder. So, we feed into this network every type of data that you can imagine, image data, time series data, spectra, scalars.
They all get combined in the entry to this input and then it's an unsupervised technique that maps through a dimensionally-reduced bottleneck layer, and back to the exact same outputs that we started with, the images, the scalars, et cetera. And by doing this, we can build this representation space that is, one, smaller in dimension than what we started with, and two, captures all of the correlations that are present, so that each node in this, each neuron in this layer represents the set of most uncorrelated directions that we can have in the space, so that we have essentially the basis for the way that we operate. Then next we want to keep and enforce physical consistency, so we often do that with a generative adversarial model, so that we have a forward model that goes from inputs and predicts, quote unquote, "fake outputs," and then a discriminator that will look at those predictions and compare them to an actual repository of experimental data and decide whether it is real or fake.
And in this adversarial relationship, if the discriminator can tell that it's fake, then that puts pressure on the forward model to get better. And if the forward model can slip something past the discriminator then that puts pressure on the discriminator to get better. And so they come into equilibrium and then we get predictions that are indistinguishable, at least by our network, from the physical data. And then finally, we enforce the notion of self consistency which we find pays big benefits in the way that we train and use these models.
And that self consistency involves the fact that often when we do an experiment we have outputs that we look at and we'd like to, in an inverse sense, infer what were the input conditions that actually generated that in the experiment that we're doing. And so we make a heavy regularization of an ill-posed inverse problem and say we prefer models that will map from the outputs back to the inputs that we started with, so that if you go from a particular x to y, the universe model ought to select back the x that we started with. Not the only way to go, but a way to go that smooths out the problem and pays dividends for us. And I'll show you that later.
So we use all the data. We try to enforce physical consistency, and we also enforce self consistency with the forward and backwards directions of our physical problems. OK, so does it work? Well, I'm here talking to you in public about it today, so yeah, it works reasonably well. In fact, it reproduces and recovers key physics information. So here, I'd like to show you some fusing balls of plasma viewed through simulated X-ray images of some relatively nice ICF implosions to see whether or not we can recover what we'd like to know about those implosions. And so on the left is a strip of true simulation outputs.
On the right are predictions made using a forward model, the one that I was just talking about. And you see that there are some things that the predictions just get correctly that are important to me as a subject matter expert. The position of the plasma in the frame, so that I know whether it's been driven harder from the top or the bottom, is about the loose confinement. The presence of edges, whether or not the brightest spot of the emission is centered within the darker edges or not, those are all captured, the general size of the implosions as you look left or right.
But there are also some errors. If you look on the left, things are going smoothly, in this image from dark, where there are no photons, up to bright. On the right, instead, depending on your screen, hopefully you can see that it goes dark to light blue to light green to yellow, and their edges that are poor approximations of the gradients that I object to as a subject matter expert. But that's OK, because not only are we keeping everything on the table, but we-- these are suited for uncertainty quantification and error prediction. So we predict the image, as well as an error map. And over here on the right is each pixel, which represents the model's uncertainty about the answer at that pixel.
So, it's very happy and everything is black where there are no photons. That's good. No plasma, no photons, that's fine. Then there are these pixels where there are errors and you see that they're correlated in these ring-like structures, which are exactly the features that I was objecting to as a subject matter expert to begin with. So, the models work, and they also tell us where they don't work.
And so our tools are not only improved here but they're prepared for statistical comparison with the experiment because I have a notion of uncertainty that comes from the forward modeling process to go along with the observations that I make in the experiment. So also, exploiting the latent space or combining the data through the autoencoder just leads to faster training and more accurate models in general. So we do this trick that I've described of using the autoencoder to combine image data and scalar data to build up this representation space where then we operate. And by doing so, we get faster, by exploiting the useful correlations from the physics that we preserve without losing them.
So if we do this process and try and produce an image, here is the loss of the error we make in an image. If we do this without the autoencoder, we take this orange path as we train over many batches, or the number of times we push data through the network, and we fall, one, relatively slowly, and two, we asymptote to an error that, if you examine as a subject matter expert the actual images that we predict, they're not very good. They're just not good enough for scientific investigation. When we engage the autoencoder we first fall very quickly.
So it takes us less data to train. And second, we asymptote to a level that's actually quite good for scientific purposes. So, we confirm our hypothesis here, that capitalizing on correlations in the latent space and the observables amongst them improves the models. It's not that shocking.
I objected to it at the top. If you keep all of the information in the image and you join it with all the information in the scalars, you ought to get better than if you throw out part of the image by taking a few features of it. So, in fact, it's true.
But it also reduces the data burden. And so we were greatly encouraged that this works. Can I quickly interrupt? Yeah, absolutely. If you can go back to the previous slide. I just have a curiosity if you can explain how the-- why the image loss with the autoencoder seems like kind of noisier, with respect to the behavior of the image loss without the autoencoder.
Do you know what that might come from? So, I didn't train it, so I don't know the exact reason. My guess is that the actual size of the mini batches is smaller in the autoencoder training than it is in the one without the autoencoder. And that probably just comes from hand tuning and trying to understand how to actually tune the network. So that's my guess, but I don't know in detail.
That would be my guess as well. Great. Yeah. We have probably hundreds, let me see-- Oh, yeah. Andrew, yeah, you want to unmute and ask your question? Hi, Brian, can you hear me? Yeah, yeah, clearly. Yeah, hi Andrew. So I wondering if you could just clarify a point here.
So, you're comparing these two cases with the autoencoder and without the autoencoder. So this model is predicting the image. Is that trick-- is that being, is the input to that model, the latent space, at the thinnest part of the autoencoder? Or are you taking the simulated output at the end of the autoencoder and then feeding that into your image predictions model? So, if I can draw your attention down here to the bottom, sort of, supervision chain.
We have a model. We build up the latent space, and then that latent space is one-to-one associated with the particular output. So we build a forward model that goes from the known input that generated the output, but predict into the latent space, and we make this loop actually work in the forward and inverse direction. And then at the very end, the last thing that we do is grab the decoder part of the autoencoder and pop back out into observable space. And then we can measure this error in the image loss space and look at it as a subject matter expert.
So that the network is trained on this lower dimensional latent space, but then we judge it in the actual decoder space, as, in an ML sense, but also as scientists. Did I get to your question? That's what we do. And I hope that answers your question. If not, you can clarify.
I think-- I'll have to think about that. Thank you. OK, now we can come back to anything later on as well.
OK, so the autoencoder-driven latent space techniques sort of clearly allow us to use experimental data more effectively. And here's an example. So, when we do an inverse problem, what we're trying to do is constrain simulation inputs based on the observations that we can make. So in the blue box here, what we have is a sequence of experimental observations that we've made in red, that's the red vertical bar.
And I haven't labeled these. These are neutron yield, ion temperature, aerial densities, et cetera. And then there's their error bar, which is the blue distribution on top of that. We can do a Markov chain Monte Carlo inversion in order to constrain the model parameters in the input space. And using just the scalar data, we get these blue distributions.
And so you'll notice that some of these are relatively well constrained, some of them are a little wider than we would prefer them to be. If we go back, instead of just training on scalars, but exploit our full latent space and use the scalars plus the image data, then we can follow this orange path. And uniformly, the distributions get narrower, and a couple of them get substantially so. And these that get substantially narrower are those that have to do with the spatial evolution of the way that the fusion products are being produced and evolving. And so instead of throwing that information away, we can capture it and we can actually constrain our models so we have a better understanding of what it actually takes for the simulation to reproduce what we saw in the experiment. So, you know, this quantifies the value of new data.
It gives you a metric that says, if what you care about is your uncertainty and your ability to constrain models, then you can propose a new diagnostic or set of diagnostics and judge their value by how much they constrain the parameters that you're interested in, which is a useful thing to do. Or it also tells you, hey look, it's much more valuable just to get five more experiments. You don't need to touch any of the diagnostics. Let's just drive down the error on the posteriors.
So it gives us a way to evaluate our facility and the eyes that we use to judge the experiment. And then we can apply those to ICF and all kinds of other scientific missions across the laboratory. OK, so here's a part where I would prefer it if we were in person sitting together in a class. I know that Cristina has seen this, so Cristina can't give away the answers. But it's fun to do and I do it with students in tutorials all the time. So depending on the situation, these networks that we're training can avoid or inherent human bias, because, what do they know? They know what they're taught and only what they taught.
So humans, even we scientists and engineers, can be distracted by context. So here's what we have. We're going to do an experiment on ourselves. You're going to try to find the toothbrush in one second. So I'm going to show you a bathroom scene, a messy one, and you're going to look for the toothbrush.
And everybody but Cristina or anyone who's seen me do this before it gets to vote and participate. So, look for a toothbrush, one second, and let me know whether you find it. Here we go. Toothbrush or no? OK, so you can say it, you can raise your hand, or just think about it privately. Did you find a toothbrush in the scene? So at this point we could look around at each other in a real room and we see that maybe half the people think they saw a toothbrush and the other half are confused that they're blind or have somehow gone insane.
So let me give you another shot. Toothbrush or no? So at that point, sometimes people are pretty sure that they've seen the toothbrush. And I will ask, did anybody see two? And maybe one or two folks in the room have actually seen two toothbrushes. And now the people who have seen none are especially feeling crazy. And people are feeling glib because they've seen two toothbrushes. So now you look at it and suddenly most people see, oh yeah, that's the one that I saw.
But also there is this gigantic toothbrush back here that almost nobody sees. And why is that? It's because your internal neural network is trained to find toothbrushes that are about the size of sunscreen and deodorant and faucets, and is in no way trained to find things that are enormous in the size of the counter. But it's even worse than that, because you're also completely filtering out things that are in the mirror because those are images and not objects. And so there's a third toothbrush potentially there. And there's even this fourth one that is obscured by an object that's really hard for you to find. But deep neural networks kind of know what toothbrushes look like.
And they just say there are two, or three, or four toothbrushes, and they're much more quickly than humans. And so there's an example of bias that that network does not have that we do have. So these are fun. We'll try one more. Is there a parking meter present? So, same game.
This will be an urban scene, the corner of a block. You can tell me or yourself privately whether or not you find a parking meter in the scene. So here you go, quick look, parking meter or no? Hard to see, so somebody maybe found it, maybe you didn't. It could be a false negative or false positive. Here we go, parking meter or no? All right, so now we go back and look.
And indeed, if you look over here there is a parking meter. Again, the same scale problem. It's four times bigger than it should be.
So your brain really does not like looking for things on scales that they should not be. There's lots of context. The world has told you how big they should be and so you're only looking for things that the world has told you.
OK, so besides these being fun, why do we do this? These trained neural networks recognize large targets that humans often miss. And that's because expectations sometimes prevent us from finding obvious patterns. So the real scientific question here is, what if we've used our simulations to build in bias? What if nature does not actually work exactly the way that we told it in simulation? We know that to be true.
So how do we get around this? So, to get rid of this bias we tend to transfer learning so that we can better match experimental data instead of missing the things that we want to see in the experiments because we told it that the simulation world just has to be the way that things evolve. So I talked about this at the top, but in this world today, simulation data is going to be blue, experimental data is going to be red. So we trained the whole neural network on simulation data that's biased, it's incorrect, because it's just an approximation of what actually happens in nature. And then we transfer it to the new context of trying to understand experiments, which for today's purposes will be objectively true. Yes, there are experimental errors.
But what we will do is take our high fidelity but very limited and expensive experimental data and retrain just this final portion of the network, keeping the rest of it fixed, and train by the simulation data. So now this tool knows both the experimental view of the world and the simulated view of the world, can make use of the theory that we've taught it, but makes corrections so that it captures what goes on in the experiments. And that does three things for us. It improves our prediction accuracy so that we get our experimental data. It requires much less data than the initial simulation data to train the actual network. And potentially, we can measure the discrepancy between these two models as a function of the input parameters.
So we can start thinking about doing physics. Why is the error between one well-trained network and the other poorly trained one a function of density squared times temperature to the fourth? And I can go back into my fusion world into an equation-of-state or a reactivity model and start understanding why my errors scale the way that they do. OK, so does this actually work? Turns out it does.
So we can adapt our learned models to experimental data to enhance their predictive capability. Here are three things that we actually care about quite substantially in inertial confinement fusion. The aerial density, which is really a stand in for how well confined the problem is. So how long are we cooking our material? That's what the areal density tells us. Ion temperature tells us how hot we're cooking the thing at.
And the neutron yield tells us how many neutrons we cooked up, basically. So here we've got plotted in all these panels a prediction from our models of a few different flavors versus the experiment. In a perfect world, we know the black y equals x line. We can make these predictions using pre-shot simulations, which are how we want the experiments to go.
And we see that, especially in the case of neutron yield, the blue pre-shot experiments are wildly optimistic compared to what the neutron yields are that we actually see. We can go to post-shot simulations where we actually simulate what we think happened in the experiment. So, the targets as delivered instead of as requested, the laser pulse as the laser actually produced it, rather than the exact platonic form that we requested.
And you could hope that those would get closer, but in the simplified physics model we're using here, it doesn't get much closer. Instead if we take the elevated model, which is the one that's partially trained on simulation data, and then retrain on a handful of experimental points, you see that the yellow points pretty much bullseye the black y equals x line. In fact, it does that almost everywhere.
It's trained on 20 of these 25 experiments, and five of these are holdouts. It's very different, it's impossible to tell which ones are holdouts versus the actual training data. But we do n-fold cross validation anyway, so it's well-trained. And you'll also note that there are some places where we miss substantially.
But those places have error bars that are gigantic. So the tool is telling us, one, I can do a better job in most places, and two, there there are places that you should be worried. And that's either because you don't have enough simulation data under those conditions, or you don't have enough experimental data under those conditions, or the simulation data and the experimental data are in such antagonism that it's next to impossible to resolve. And so you've got to figure out something that's going on there. Nevertheless, be careful with where you're going. So the single model holds across all of our shots and all of our observables.
And it gives us a tool for doing better design of the experiment in the future than the naive simulation model by itself. So, keeping up with a theme in this talk, no data is left behind. So we don't do this just for scalar data but we do it for images as well.
That's one of the things that that autoencoding latent space does for us. So we can take the scalar data in this a little bit more aggressive NIF application. That was at the Omega laser at the Laboratory for Laser Energetics. This is at full-scale NIF data. And you can see here again, predictions versus the actual measurement in the simulated and experimental data. Red are simulations for testing and, sorry, red are test data, green are training data.
We can move them onto, closer to the y equals x line. We can take out these sort of pathological nonlinearities. The world is getting slightly better.
This is only with 20 experimental data points. So, lots of simulation data, very rare experimental data, and we can do the same thing for the images. So here are actual X-ray images of fusing plasmas from NIF experiments.
These are simulations with a relatively naive simulator. And so you can see, the biggest objection is that the brightnesses are completely wrong, and the growth shape. This is an axis-symmetric sausage, if you will. This is nearly spherical because we tuned it to be so. It's also left-right asymmetric because it's a three-dimensional feature. And there are filled tubes in the capsule that we use to load the fusion fuel that are making bright spots.
Our prediction, that has been transfer-learned on these actual images, and again, these are test images, not training images. Our prediction, which has never seen this experiment, has learned that this experiment should be mostly around left-right asymmetric and that there are 3D features that are almost always present in these experiments. So this is not perfectly ready for prime-time physics use.
But we're getting it to the place where we can start to capture features that are present in the experiment but absent from the simulation. And we can start to put them back into the AI or CogSim prediction. So it's sort of satisfying to move that forward. In the transfer-learning world I'll mention one more effort before moving on to some other ideas here. We've also built an improved experimental prediction pipeline that corrects the simulation models using all of the fusion experiments that we've done on NIF.
So, exploiting this autoencoding structure and building them instantly reduced latent space. We've engineered a latent space that uses about 300,000 simulations of the fusion capsule only. And then using that latent space as a place that we project into, we can take much more expensive simulations that involve laser propagation, heating the X-ray bath that we produce using the hohlraum, and then doing the compression of the capsule, we can project into this common reduced dimensional space, which is just the space of burning plasma, is what do they actually look like, and come back to our predicted outputs. And here we show on the right that if we had been running this process for the whole history of NIF, we could take our simulation improvements and have relatively huge errors back, as far back as say, 2011. And then if we'd been transfer-learning, shot after shot after shot after shot, we would have, after seven to 10 shots on NIF, have gotten to much smaller errors. And then eventually we get to a place where the error is sort of at the 10% to 20% here.
10% to 20% errors are pretty good, given that hand-tuned codes or variation on the machine can be 20% or 30%. So just another example of the way that using the multimodal data together helps us, one, take advantage of all of the simulations that we have done over a long period of time, as well as the long body of experimental data, and put it together in a space that actually makes physical sense. And then we can use it as a gauge for both how well we're improving the simulations themselves, predicting the space, but also the global AI model that we use to make these predictions. So it becomes a tool for us to measure how predictive we're getting and whether we're improving as a function of time. Let me just say that you're halfway through.
And we have also a question for you if you'd like to answer that right now. Yeah, I'd love to. So Ashgan was saying, was asking, what could be the reason or reasons for the neutron yield, the discrepancy between the experimental and predictive model? I think from a couple of slides ago. Yeah, that is the reason that we exist in the ICF modeling world. What's the difference between our simulations and our experiments? So we go back, and in the paper that supports this by Kelly Humbert, she goes back and she tears apart the physics reasoning for what's going on.
And without going into the details very explicitly, what we find is that these simulations, excuse me, these simulations are missing fundamental laser plasma interaction effects that change the shape of the implosion. And so if you go back and you capture that laser plasma interaction you can greatly improve the yield. And the transfer learning exercise here is implicitly learning that laser plasma interaction physics from the data rather than from adding the additional physics package. And so we've learned that there's some missing physics that has to be included. We suspected that in advance.
It was not a complete surprise. But the surprise was that we could learn that physics from the data. And then we could go back and do simulations with it in place and then close the loop and find that reduces the discrepancy. So it's a nice example of being able to test and then failing to disprove a physics hypothesis, so that we essentially confirm it and can move forward. Was there something else or is that it? No, I think that's it for now. Thanks.
OK, variations on that theme. So doing that at NIF, here's another way to say the same thing that I was sharing with you earlier. On NIF experiments it's very important to implode the shell so that things stay spherical.
If you get a aspherical perturbations, that causes weak spots that allow pressure vents and allow the fusion products to leak out of the confining cold shell. And so these long wavelength perturbations, having this be shaped more like a pancake or more like a sausage, is really damaging to the implosion. And we characterize that by the Legendre decomposition of, say, a feature, a contour like the white contour here, and decompose that into those modes. If you look over here on the right at the NIF, our transfer learning tools have noticed that the prediction compared to the shape of the X-ray image, the second Legendre mode divided by its steady state average, roughly how pancake, how sausage shaped is it compared to how pancake shaped is it? The simulation alone if we do this without full physics turned on, which is too expensive, has really no clue what shape the implosion ought to be when we fired at the experimental facility.
But when we do the transfer learning it has learned very closely the yields get much better. But if we dig in here, what it's actually figured out is what should the shape of the implosion be. So if you look down here at the bottom right, here's a visual representation of what's actually going on.
In green is the simulation prediction of the shape of the implosion. In orange is the actual experiment. And in blue is the AI model that has been trained on other data but is predicting this data as unseen hold-out data. So what I want you to see is that the green is very different from the orange almost everywhere. The AI model, the blue, in all cases moves much closer from the green towards the orange. And in most cases, the blue and the orange shrink wrap each other, meaning the AI model has learned that, given the inputs that we give to the laser facility, this is the sphericity that we're going to see in the output.
So it's discovered what the shape model, the appropriate shape model is for the actual facility. Now, the underlying physics that's driving that gets very complicated. It goes to laser plasma interactions. It goes to asymmetries in the radiation environment and all kinds of things which we can dig into further.
So the question of why did it learn that is a more detailed question that we continue to engage on. OK, so where do we go with this? I mentioned at the top that we need these tools and techniques, but we also need the computational platforms that underlie them. And the things we do here are relatively strenuous when it comes to computational environments. So our newest and largest computers are enabling machine learning at an unprecedented scale for us. So what we did was generate 100 million ICF implosion simulations. So, 1.5 billion scalar outputs, 4.8 billion scalar images.
And we built a state of the art machine learning solution on top of this. These models I've been talking about, we trained them on this enormous data set. But we're not keeping those to ourselves. The point of this is to drive conversations like the one we're having today.
We're hosting a shareable data set for machine learning, which you can go find down here at our open data initiative, and along with some free training solutions that are there in Jupyter Notebooks. So if you don't have access to the world's largest supercomputer, you can have our data. Now, on the website is 10,000 of these samples, not a hundred million of them, because I don't know how to put that in a place where you can just download it. But if you're legitimately interested in a larger amount of samples you can contact me directly and we can make that available to you. If you're collaborating with us you can get access to our facility. Or in the worst case, we can figure out how to buy a few hard drives and we can move stuff around and can actually get it to you as a product.
It's shared through the University of California at San Diego and it's there for you to go explore openly and do what you like with. So what we are using that for is to understand what is the scale that we need to operate at as a scientific facility. And so we've got them now, we've got our computers now operating at pretty singular scales for applied science.
Here what I'm showing you is a history of training, the largest neural networks going back to just a couple of years ago. The vertical axis is an extensive quantity, the number of petaflop per second days. So that's like kilowatt hours. It's how many operations did it actually take to train these networks.
Along the horizontal axis is the calendar year. And you can see that the number, the amount of compute that's required to train these things has been doubling about every 3 and 1/2 months. Notably, far faster than Moore's law, so computers are not going to directly keep up with this forever. And what we've done is make a concerted effort, starting back in 2018, to train on, say, 10,000 samples-- excuse me, sorry, I've been talking a lot this morning, to train on 10,000 samples. And then slowly work our way up to 100,000, a million.
And we've been training over the last couple of years using the entire Sierra supercomputer, the third largest in the world, to train for between a full hour and a full day, so that we're sort of rivaling the kinds of networks that we know from the past couple of years. And yes, industry continues to skyrocket up. And we've actually decided that now that we know we can do this, we're trying to go back down the other direction.
We would like not to have to use lots of carbon, lots of energy, lots of power and money, to train these neural networks, but are instead trying to get to results that we can get on this data with much more data economical measures, of which the autoencoder that we talked about at the beginning is a way to buy down the cost in these things and use less data, fewer passes and mini-batches through the network. OK, looking at the time, I think I will jump past this and just say commerce wants from a next generation computer something that might be different than what we want. And in this community we have to be careful. So, the Googles, the Amazons, the Facebooks, they want to do infrequent high-cost training. They're going to train Siri.
They're going to deploy it on your phone. And then they want to do very frequent low-cost evaluation, on lightweight processes, on heavyweight processors, you name it. Instead we're doing something very often that's very different.
So frequent low-cost training, but less frequent evaluation than what they're doing. Because we want to do training. We want to have hypothesis. We want to say, oh, I think I learned this about the physics I'm going to change my model. And now I've got to retrain. And so it's potentially a very different operation.
And we're engaging in co-design with vendor partners in order to know what those computers ought to look like. And here's an example of a physics problem we're using to drive this forward. So new AI-driven computing methods might change the architectures we're used to in this way. Here is a schematic of a Radhydro code that we use to predict fusion products at Lawrence Livermore.
So we pay attention to injection of laser light, the production of magnetic fields, transport of electrons. And the package I want to focus on here is the atomic physics that we do with a tool called Cretin. So you, you know what the radiative field is, you know the density of the temperature.
You can compute what the opacity is so that you can do radiation transport in the code. This, in hohlraum simulations can be up to half of the wall clock time that we use in the simulation, just doing detailed atomic configuration accounting. So instead what we have done is train on the atomic physics data. We do this up front and build a model with neural networks on top of this, so that at runtime, we don't have to do the expensive calculation. We've already done that and banked it in advance.
And now we just do the quick AI call and evaluate that very lightweight neural network. So we can replace expensive finite-difference physics packages with the fast AI surrogate. And so what does that look like? It looks like replacing this physics complexity and computational costs with a much more effective model.
So here are some, in the atomic physics, world models that you'll be familiar with, detailed configuration arrays, SCRAM, ATOMIC, ENRICO. These things take hours to days to get just the answer for a single time-step and a single zone and a Radhydro code. And what we've done is take this very expensive DCA code and made it, instead of taking in our application, seconds, down to a few tens of milliseconds, and also driven up the number of levels that we can actually account for and have a much better understanding of the ionization state and the atomic properties. We've trained a deep neural network on that model. And then we can use that to produce the absorption and emission spectra with very detailed representation of line shapes and the atomic physics that we're trying to capture. And this is all well and good.
In our HYDRA tests with the hohlraum simulation, admittedly chosen to highlight the benefits, we get a 6 and 1/2 times speed up in this problem that we're working, by taking advantage of all this compute done in advance but embedding it with a deep neural network inside our code to accelerate it on demand when we need it. In reality, I think this number is going to slip down to more like 2x when it's not a cherry-picked problem that we've chosen just to demonstrate how good this can be. Making the largest supercomputer in the world a factor of 2 bigger is like a $300 million proposition. So that's kind of good.
We'll take the factor of two speed-up. So the other thing that we've done is, and this is a taste of things that you can get if you keep working in this area, is we partnered with Cerebras, a start-up company in Silicon Valley who we happen to be physically close to. They produce the largest chips on the planet. So this is, if you can imagine a silicon wafer cut from a bowl that is a circle, these are the edges lopped off. And this is the biggest square that you can inscribe inside one of those wafers.
This is a huge chip that consumes lots of power. But it's very quick and designed for AI training and inference. And we've connected that to the Lassen supercomputer which is the number 10 supercomputer in the world and the unclassified version of the Sierra one that I talked about earlier.
And we've shown that you can get throughput for these Cretin model evaluations, the atomic physics I'm talking about, that is sort of 37 times faster. We already had gotten ourselves a factor of 2 faster. Speeding up these evaluations is going to get us, is going to get us even more. And we're going to see how that works out. But we're really shaking out what the next generation of supercomputers at DOE labs and facilities are going to look like.
They're going to look like high-precision processors for doing precision simulation and doing the transport of momentum and the detailed physics processing, coupled to these heterogeneous compute centers that are made specifically for AI and machine learning. And so we're constantly adapting to these cutting edge changes in HPC, trying to answer these questions. What computer do we need for our most ambitious applications next? And then what can we do with the machine once it arrives? And so an example of this is the El Capitan supercomputer is going to land in my backyard in about a year or two. Not actually my home, of course, but at Lawrence Livermore.
So about the size of two tennis courts, the machine is going to be capable of about 2.6 exaflops. So it's a big machine. It's about 20 times bigger than the biggest computer you can get your hands on right now. And we're working on these fusion-driven applications in AI to put this thing through its paces as soon as it arrives. So just to give you a highlight of what we do before I wrap up here, we're going to capture a bunch of digital stars to try to design a new optimal one. So essentially we do lots of simulations that digitally freeze high-fidelity ICF implosions.
On El Capitan, rather than doing it in 2D like we have in the past, we're going to work our way up to 3D simulations routinely on this machine, because it's just so capable. We're going to take these tools that I've been talking about for transfer learning and combine that with the NIF experimental database and then produce an optimal design in silico. So this is not that different from taking a public database of celebrity images and then generating these deep fakes that have never existed but are plausible and maybe even attractive as new options. And the difference is on the scientific route, we're going to use a real NIF experiment to realize this optimal-generated implosion which is maybe a better solution than trying to actually make a new celebrity, not quite sure how we would go about doing that. But this is both really engaging science. It answers the question of, how can we drive the mission forward with a new computer? It will tell us what the limitations are so that we can design the next generation of what's coming.
And to be frank, it's just super fun. You get to use the largest experimental facilities and the largest computers in the world to do cutting edge AI research to move the whole endeavor forward. And it's just really exciting. And with that, I'll end on the last bit of excitement. In our laboratory, hopefully it's made the rounds in the fusion community, we just on August 8, fired a shot at NIF where we got 1.3 megajoules of yield driven by 1.9 megajoules of input laser.
And so while it used 1.9 megajoules of input laser, the actual energy that we capsuled, coupled to the fuel, I mean, to the capsule that we're driving, we produced about five times more energy than what was coupled with the capsule. So the capsule has no idea how big the laser is in reality. What the physics knows is that, for an input of unit 1, we produced an output of unit 5. That's a first time. And so this is about eight times more energy than what we had in the previous burning plasma.
And compared to where we were a year ago, we're about 25 times higher up. And for this community, you'll recognize the Lawson criterion. We can define a notion of generalized Lawson criterion for ICF. And we've slowly, over my 17 years and the 10 years that we've been firing NIF, been walking up campaign by campaign as we have new ideas and innovation. And as the threshold phenomenon of igniting has turned on, we have just made this huge breakthrough leap.
And by all definitions except the one by the National Academy of Sciences this is an ignited plasma. The NAS definition required that we produce more energy than what we used in laser, so we've got another 30% to 40% to go. Nevertheless, we're quite excited. OK, so beyond just being happy about that, it ties back to our actual AI applications, because we're using the techniques that I talked about to try to understand what's going on with this shot and its siblings. And so we do the AI-driven inference that I've been talking about to help us understand exactly what happened in the target chamber. And right now we are as far along as the predecessor shot, to that nearly igniting shot, which produced only 0.17 megajoules.
But here we were able to constrain the model to tell us what happened on the predecessor shot. And if you look here just as an i-chart, this is the yield, the ion temperature, the aerial density, the time that the thing actually bangs. Here's the experiment. Here's a typical post-shot simulation. And then here is what we call the Bayesian-Super-Postshot.
It's our AI-driven inference. And you'll notice that these are all very tight approximations of what's actually happening and well within error bars. And we find that we get nice constrained distributions of things that really matter for the implosion, like how long the implosion continues to coast after we've stopped driving it with the laser. And so we are able to say that with our AI techniques we know that we were coasting for something like 1.4 nanoseconds before the thing banged. And we know that the shorter this is in simulation the better it does.
We're starting to get inferences that on the next shot that we did that got very close to igniting, that we drove this down by about 300 picoseconds. That was the goal in the experiment and now we're working to go back and infer what the distribution of coast times is for this new one, using the tools that I've talked about with you today. So with that, I think I'll end. And I know we've got at least a few minutes for questions, a little bit longer, but we answered some in-flight. We're always looking for the best and the brightest.
So there's a room full of the best and the brightest here listening to me talk. And what I would really like is to listen to you for the better part of your career. So, we have a Data Science Institute where people can come and partner with us for the short-term, or it's our pipeline to long-term hiring. I'd encourage you to go take a look if you're interested in the kinds of things we're talking about here. At Lawrence Livermore we bring over 1,000 students onto our 7,000-person campus every summer.
And so the mean age of our population goes down dramatically for the summer and comes back up when everyone goes back to their campuses. But we also bring in a couple hundred folks to our Data Science Institute. So please follow the link and express your interest. I'd love to work with you. And with that, I'm going to turn the floor back over to Cristina and we can have questions. And I appreciate your time.
Thank you, Brian. It was a great talk as always. It was really dense in material and achievements. Yeah, great, great. You're definitely getting claps on Zoom. All right, so do we have any questions for Brian? I have at least one.
And I'll save it, if there are any other takers? OK, I'll start with my question then. So you mentioned these autoencoders used for analyzing all these huge data sets that you have and these kinds-- so, and just to give an idea, how many parameters do these, how big are these autoencoders? Yeah, they vary. Sometimes they don't have to be very large, sometimes they're relatively large. When they're convolutional, the convolutional part that takes in the image, I guess we typically break those down into roughly 100 by 100 images. So there are, what, 10 to the 4 input neurons for the image and then we have another few scalars. So it's roughly 10,000 might be the computational width of the first layer.
And then maybe there are, depending, there are two to five or six layers in the encoder and then symmetric on the decoder part. And the bottleneck we usually come down to a dimension that is in the tens of neurons. So how many total parameters? Well it's the weights and the bias for five layers, going from 10,000 pretty much linearly down to 10 or so, with some art in between to try to understand what the architecture ought to look like.
So what's a good number? That's, I don't know, a few tens of thousands of weights and biases, more or less. But a nice follow in discussion is there's really not good theory for how to size that network. Right. Or how to build the architecture. So a very clever postdoc that's working with us, named Eugene Kerr, is working on a tool that takes an existing neural network and does essentially some unsupervised error analysis to say, which layer is suffering the most? Where am I making the biggest errors? And then you can go back and preferentially modify that most ill-behaving layer and essentially do adaptive reconfiguration of the network so that where to transfer learn.
So the poorest behaved network is the one you should better inform with experimental data. And in fact, if you can shrink that layer then you require less experimental data. And so he's working hard to try to understand really the heart of your question, which is how many parameters should there be and how should I distributed them over the network so they can do a good job of predicting things.
Yeah, and also, I'm assuming you're also saving computational costs of training huge architectures when you may just need fewer layers or fewer parameters, right? That's right. Yeah, one of the things that I'm sometimes shocked at is, when we don't know what we're doing
2022-09-22