Faculty Forum Online: Mingda Li PhD '15
Hi i'm whitney espic the ceo of the mit alumni association. And i hope you enjoy this digital production, created for alumni, and friends like you. Welcome to the mit, faculty, forum, online. My name is edith one i'm from the department, of nuclear science and engineering. And i will be the moderator, for today's event. This broadcast, is sponsored in part by the mit federal credit union, mit professional, education. And mit sloan executive, education. I'd like to give a special welcome, to anyone, from those units on mit as well as a special welcome to our colleagues from the department of nuclear science and engineering. And the ans. A reminder, that after we hear from today's guest we'll field your questions for him. Please use the q a feature, on your zoom tokubar. Ask them and we'll get to as many questions as we can. Today we'll hear from professor, ming dali. He holds a professor, a phd, from mit. Earned in 2015. And he's the norman c rasmussen, assistant professor, in the mit department of nuclear, science and engineering. We'll post a link to his full bio in the chat now. Professor lee's talk today is entitled. A tale of two singularities. Fundamental. And energy applications, on topological. Wild materials. Welcome professor, lee. Yeah thank you eddie, for the introduction. And uh, hi everyone. Welcome, back mit. Even, virtually. So let me share my. Screen. So, today, we are going to talk about. A type of topological. Materials. Uh called the wild semi-metal. So in the past decade, there have been really numerous, researches, on topological. Materials. For applications. Like, electronics. Without, energy dissipation. Or for quantum computing, on information. Applications. But today. Is a specific, type, of the, topological. Material, called the wild semi-metal. Driven, by a pair of two, singularities. So the structure, for today's presentation. I'll first, give a, crash course, on the introduction. On topology. And their links, to this type of materials. And give two examples, from our recent, research. One is more fundamental. How we can visualize. The topology. Of electrons. From the ionic, given freedom. And the other, how we can, use this singularity. As a source, to harvest the energy. So first, the topology. So a very common. Or. Like even cliche, examples. Is like. The cups, with a handle, it's just topologically. Equivalent, to a donut, because they both share. One. This hose. But today i'd like to provide a few more examples. In this area. So the first thing, the problem is actually, quite close related, to geometry. So here is an impossible, paper trick, so how can we, make a paper, cut like this. I just one single paper no glue. And the other examples, when we try to hold the piece up and we don't want to hold it like this, but we want to fold it, along this edge, so it gains some rigidity. And, all the way to the teeth. So to see why this is the case, so here actually the two sides they are back in the front. Side of the paper, orientation, matters. And the right example. So it has a flat, curvature. So, if when it's flat, and even we twist it a little bit, it wants to maintain. This flat curvature, that's. Against. The rigidity, all the way, to the pita tip. So the linking to the topology. That's if we, make it deform, higher, that means it's also linked, to, a continuous, deformation. So imagine there is a very strong carbine. So he may be strong enough to lasso, a horse, to put a lava, here and even multiple.
Ones. But may even have hard time to lasso a basketball. So all these lasso will just keep shrinking, shrinking, all the way down to a single point. So this is a very. Typical, topological. Phenomenon. The lasso is a circle, called s1. And put a lasso on the horse neck which is another circle. We get. This so-called, first. Homotopic. That's a number of environment. Distinct. Ways, to deform. And it gets different like integer. Types. And if we lasso this. Circle, on the sphere, we get a trivial number of zero. So we might think okay this is really real life not directly related to physics. But imagine, if we generated, this 1d example. To two dimensional. Then it directly, gives the so-called, integer, quantum hall effect, and this c as integer, is just the, this number. Integer number, in quantum heart factor. But today. So the type of the topology. And later you will see which can directly, link. To the, uh this wild semi-metal. With sharing exactly, the same mass is by asking this question. So why almost, everyone, has a this has, role or kind of careful. On the head, so that's a topological, similarity. So to truly fully understand, this question. Let's do, some background, introduction. So we have a continuous. Curve. And we can define a local curvature. So imagine, if there is a. Circle let's make it a tangent, in this local area, and curvature, is just one over this circle radius, r. Imagine, it's not a one-dimensional. Circle, of curve but have a two-dimensional. Surface. And we can generalize, the curvature, to the so-called, gaussian curvature. For, cylinder. And we have this two principle. Directions, a and b and reduction, curvature is just the product, between these two. Uh directions. And because, we know that one direction, is really flat, the gaussian curvature is zero. That's also the reason, why, this is beta, originally, before we, uh, just uh tweak it it's a very, gaussian curvature. After tweaking, it to try to maintain the zero function curvature. And against the rigidity, along the radial direction. And here what's related, to the one semi-metal. Is on the sphere. And everywhere, the curvature is just one over r so we get a gaussian curvature. One over, r squared. And from there. We can define a quantity, called the ola characteristic. We have a closer, sphere. And then just integrate, the gaussian curvature, over the entire, sphere. And divide, by a factor of two pi. And that ola characteristic. Of chi. Becomes, an integer. And it has a physical. That's the number of total, singularities. On that surface. And for. This a sphere. Function curvature is just, one over r square everywhere. And we know spherical. The surface is four pi r square, divided by 2 pi we get the two similarities. On the field. And that directly, explains. On the sphere, and if there is some vector field, on top of it, and there are two singularities. And the head is almost like a hemisphere. And, almost everyone has this one singularity. And if we consider, our hair some vector field, on this, spherical, surface. So very interestingly. So this type of topology. Shares exactly the same mass, to the materials, we want to introduce, today, so that's the, topological, one sending methods. So here's the transition. So in the higher hole, topology. So we are talking about a two-dimensional. Spherical. Surface. That's in real space, our space. And we all know we can do a fourier transform. And in momentum, space. In one sentence method, there's also some. Severe, in momentum, space. And just like, we know there's some gaussian curvature, in the 2d. Spherical, space. And, in this 2d momentum, space, by computing, quantum mechanics, will function. We can also define, something called the barriculature. And we call it f. And just like we have all our characteristics. On this 2d surface. Here, we also have an environment. Like a. Number or we can call it pyrolytic, here, it's just, integrating. Over the the surface. Not in real space, but in momentum, space. So consequentially. We obtain, a pair, of these. This is, while, singularities. Which turned like a round note. And they paired because they all. Have this opposite. This chirology. You can consider, like a light which have some. Leftover polarized, and white polarized, light, and here for wildfirming. The lactobacilli. And, this light technology. So that's. The source, of this, one from the materials, with this kind of singularity. And the linear, destructive. Energy momentum, relation. That's defined. Metal. So to see how this works metal are why they are interesting, so here are a few fundamental. Examples. So one is. Chiral, anomaly. So that is the breaking, of the fundamental. Like. Symmetry, which happened only, in, high energy physics, but now, realized.
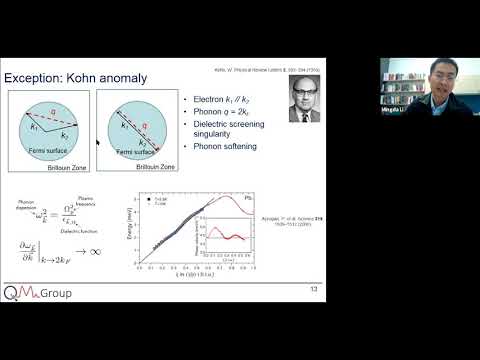
In Canada, matter systems. And there are also some special, circuit state, fully topological. And protected. And that can be used to build a high performance, electronics. And there are also some singularity. To giant. The thermoelectric. Energy. By the question the first question, we want to confirm, that materials. It is a wax and metal as a very first step to further experimental. Studies. A typical, step. To confirm, the materials. Is a wireless, method. It's a combined. Uh initial calculation. And called this, angular, resolve the photon emission. This method. Are test. So from this. This sense of function of initial calculation. So people can obtain. The band structure, you can see this linear dispersive, with this welcome. And here there's some singularity. And then carry out the photo ignition, measurements. And see this. Bands directly. But there are some, limitations. So such as this, the type of the materials, they are very limited. They have to clean cleavage, into like a atomically. Sharp. Surface, in order to allow this kind of measurements. And we cannot, easy to add, some like a strain, or magnetic, field that will disturb, other signals. Or they also have a very high technical, barrier. Such as really need to maintain, very. Ultra high weapon. So the idea, here. So can we. Really try to detect. The topology. Of this wildfirming. For this electronically. Level freedom. By detecting. The ionic. Default freedom. So the answer, briefly, is yes, if we can, fully take advantage, of these, singularities. So to see. How that works. And. We know that the ionic, critical freedom, the basic, quality particles, they are phonon. And the electronics. And when they link to phonon, they are linked by electron, phonon interaction. So electron, phonon inhabition, is really, ubiquitous. In, many materials. So such as happening, in determining. Like a, resistivity. In metals, for carrier mobility, in semiconductor. Also can assisted. Some. Electronic. Transition. Or contact information, processing. Diamond, mv center, or even this conversion, of phono media, superconductors. And here. In the current. Context. But we know that some limitations. Of all these examples. The conventional. Electron, phonon coupling, these strands. Is very weak. So, if we use some, dimensional. Constant. A dimensionless, constant is almost, less than, a one over one hundred. Very small, amounts. Of the interaction, stuff. But there is one actually, an exception. Called common normally. So the watercolumn. Is one of the pioneers, also developed, intensive, functional, theory. But the common normally works like this, but imagine we have a macro, as described. By a fermi surface. And the one electron. With the momentum. There is. A k1. And after scattering, with a phonon, uh, like the vector q, scattered, into another. Electron, becomes, the. Momentum, peak. And the congo normally happens at a very special, condition. That means, if the k1 and k2 they become parallel to each other. Because. These are like a periodic. And these two are points are nested with each other, let's appear like there's. No. Scattering, at all, that's leads to a, sharp divergent, change on the bilateral. Function. And. That will cause a shortening. Of the phonon, energy, and that's observed. In some materials, like a lab in this particular, example. But here we don't have a fermi surface, it's no longer, metal. But it's a. One semi-metal. With a few disjointed. Uh this topological. Singularities. So can we induce a chromosomal. Inner world and network. So in our very recent work and we provided, the answer, as saying yes. So here is how. We, did it as well. So to show, there is indeed a common normally, in the wild, metal, so we first want to provide, a theoretical. Prediction. Of the reservation. Criteria. So where we want to expect a common nominee to happen. So after, some, quantum field theoretical. Polarization. Calculations. So, we get a very simple criteria. So assuming. If we have the two different, uh, while cons, these two are two singularities. Located, in momentum, space, kw1. Kw2. And if, the phonon, with bigger vector, q, will link them together. And the phonon, energy will also accept, the foundation. And it will generate, the chrono normally. And and this sonar energy assistance. Is to this, dynamical. Effect. So comparing, to the conventional. Anomaly, here there are a few. Distinct. Features. So one, is chirology, selection. So because. Electron, phonon coupling, it preserves. This. This chirology. And, if there are two wow cones. Only when they share the same chirology. Like a writer chiral, red chiral, or leftover. To left tyro. Then the transition, becomes, possible. If they have opposite, character. Then the transition, comes from. And nature will see we can effectively.
Test These predictions. So the second, is that. In some materials. Like a conventional, method. The divergence, is like a logarithmic. In some two-dimensional. Electron, gas like a graphene. There's also kung anomaly, but with some one over square root of the divergence. And in the wild cemetery. Generation, shows that there's. A strong really power long divergence. And consequentially. So the soft turning is not happening, only at a single point, but also softening, can happen at the nearby. Momentum. Of space like this bow shaped, opening. Whenever congo normally happens, the funnel energy, will just be. Dropped. And, so, with this kind of theoretical. Guidance, then we can start to, prepare, for the experiment. So for a particular, type of the wild semi-micro. So we choose, tandem, phosphine. Tap. The reason is very simple. It's a very clean system that only hosts, two types. Of these, while clones we can call them w1. Type, and double, two times, not only two but they have, like a 24, in total, in the momentum, space, but they're just, located. Separately. In the momentum, space. And then in order to carry out this bonus measurements. We also need, uh, a, high quality, large single crystal. So we spent almost, four and a year of effort to try to, find the recipe. To grow, really, large centimeters, size of the crystal. That's like a order of magnitude, larger than, literature, reports. And then we can. Provide, this high quality experimental. Signatures. And for this particular. Of material. There's also one more interesting, feature. We want to show that at the phone number vector q, as the difference, between, two types of the one node of kw1, kw2. And that's a, wave vector, q value that will be common normally. But that value is happened to be another. Kw2. Type of the one node. So that gives a very specific. Uh kind of, a prediction, condition. And we would expect, congo normally happen, at a, around, node, in kw2, itself, but not in kw, one time, of the well known. So among, all these three dimensional. Uh brilliant zone of momentum, space, we expect, a quantum number pattern as a single. And this very specific. Wave vector. Let's see how we see that. So this is, this common normally, experiment. So if we have the two different, singularities. W1, and w2. And assisted, by the phonon, with the specific. Vector q, and linking them together. That's how we observe, this phone in softness. And see them in the. Original, spectrum. Of after, blocking, we can also see that, this significant. Two three. Milli av this phonon sharpening, compound to this nearby. Magnitude. And this. This, theory. Predicts. This criteria. And that criteria, is metal with very high, precision. The less than one percent, of the error. And comparing. With the theory, with, the bow shape, we don't have too many. Points but we can see generally, there is some. Softening. Like a bow shaped. Parabolic. This alternate, is also being, observed. So contrary, to that. If we go to another w1. Type of the while node. And which, link the two different. W2, types of the while node, we won't be expecting. A. The reason is that. This, is linking, these two w to one nodes, uh, to meet this momentum, energy conservation. They must have different, uh, uh, this chirology, operating, technologies. That's why we wouldn't see any softening, profile. There. So that's, our main, experimental. Findings. Showing that, this, electronic. Topology. Singularity. Stopped in the phone. So there are a few, possible, applications. Using this common normally. The director. Consequently. We can measure, the electron, phonon interaction, strength. Because, that is the parameter. That determines, like a decoherence. Of the quantum state, and that's also one reason why many quantum phenomena, cannot be, observed, at room temperature. So that we hope that can be useful. And to. Indicate, what kind of quantum material, with some kind of weak, electron, phonon interaction, can possibly, have higher temperature. Applications. The other the other more. Technological. Relevance, is on the so-called, general electronics. So just like us to be in tronics, people use like, electron, spin apps been done equal freedom. So that, term. In the past, two years, try to use the. Left, chiro, or rhinocarol. Types, of the, charge carriers. In order to. Build electronics. And because in the current, context, only the chirology, conserve the scattering, is possible. There is some priority, dependent. Electrical, transport, there. But still overall, this example, is more fundamental. They are, more practical, use, utilizing. These similarities. So that's actually our. Main topic for today and kept us very exciting, in the, past few months. So that's about. Using, this, singularity. To really. Harvest, the thermoelectric.
Energy, And breaking, the, this. Upper limit by order of magnitude. So thermoelectrics. Is a way, to, convert, like a waste heat directly. Into this useful, electricity. So the overall, efficiency. Directly, linked to a dimensionless. With a customer, called the ct. It's proportional, to temperature, t, and proportional, to this so-called, thermal power, s. It's just to have a unit, of volt per degree, that means, by. Varying, the temperature. Difference. For one, degree, how much voltage we can gain, and it's proportional, to s square. And then it's proportional, to the electrical, conductivity. But inversely, proportional, to thermal conductivity. Intuitive, understanding, if we, have some materials. With low thermal conductivity. That reduce, the thermal, loss, and then can help to preserve, the heat in order to facilitate. The energy conversion. For the majority, of the effort. In the thermal electrical, community. Is to separate, the sigma. To k, so that's a so-called, electron, crystal. Phonon glass. The reason is that, they have two have very different, mean free paths. So in many materials. The phonon can get strongly, scattered, in this lack of polygrams. And green boundaries. But electrons, can penetrate. Through, and that can significantly. Reduce system conductivity. K but not to lose too much on the electrical, conductivity. But, less attention will trade on the overall, factor, called the acid, square. Sigma. And that's called the power factor, because there are some fundamental, upper limit exists. So here's why. To see why. There's some upper limits, let's first mention, so why metals. They are not, good thermoelectrics. So metals have a very high, like electrical, conductivity. As we all know. However. The metal has very low, thermal power. Because the thermal power, intuitive, is actually a measure of, entropy, with just a different unit. They want to convert, some. This heat, into. This electricity. Then it has to be enough, available, states, for the carriers, to jump into, that means it has to have high.
Entropy. But here imagine, this is the fermi surface, of the metal. And the metal only have this small. Range of really active, carriers. Near. The fermi level ef. So the feedback of the thermal power is very very small, so metal have very low ct, never almost a good, thermoelectric. So that's why the majority, of the thermoelectrics. They are semiconductors. The sigma. The electrical, conductivity. Is compromised. Not too high, but it can gain very high. This thermal power. So if we plug them together, so this is so called a, wrinkle plot. As a function, of this carrier, density, higher and higher this electron. This, density. We know that the. Electro, conductivity. Will increase. But. It has less, entropy. And this thermal power will decrease. And if we, put them together. Multiply. S square sigma, there's some optimized. Peak value. And that is this fundamental. Limit, which makes it very hard to significantly. Increase. Uh power factor. And there's one more thing was not mentioned, this, as, uh, if we have really random, this particles, electrons, just like ideal, gas, it's just like a kb, over, e, so which has this, highly. Randomized. This carrier to have a high, thermal power. And so the recently. This one physics professor. Yang fu in physics department. So he made a few predictions. So. Preserve, some, like, theoretical, guidance, how we can use, the topological, singularity. In the wild, metal, to break the barrier. So the first thing. So they show that, the high thermal product can be generalized, can be generated. At a very high magnetic, field. So for conventional, material, if we apply a external, magnetic, field, there will be some saturation. But, this, while semi-metal. It will keep growing, when we increase, magnetic, field. And the reason for that, is largely, related, to a so-called. Quantized. Thermoelectric. Heart effect. So we know quantum hall effect, the whole electrical. Conductance. Is a universal, constant. So in this example. So this alpha, x y is called a thermoelectrical. Hall connectivity. That's the transverse. Thermal current, over longitudinal. Electrical current over temperature. That, will reach to a universal, constant, and this is the number of the welcome, that's the fermi velocity, and then all the rest are universal, constant. And. So he showed that if we want to make this happen, the transverse. Thermoelectric. Heart and the transverse.
Resistance. Will have to dominate, the longitudinal. Thermal power, this is very contrary, to conventional, material. Longitudinal. Power is dominated, by, longitudinal. Thermal electrical, response. And, another thing. So when we apply magnetic, field, there becomes a problem, called localization. So that's just from the lorenzo, force. The this charger carriers, will experience, a force so, uh, this perpendicular. To the moving direction. That's why the electrons, will tend to have this circular. Motions. And then. This electrical, resistivity, will be increased, significantly. But for the wire same metal. As we know there are two, hair holes, in the momentum, space, and very robust, and cannot break. And this make it a, remain, metallic, state, and reduce, the longitudinal. Resistivity. So that's a little bit, tricky, but, here in the summary. We have a quantized. Value of thermoelectric. Conductivity. One is dominant. There can be a high thermal, power, which means high voltage, being per temperature, gradient. And if we can still make it maintain. Low. With longitudinal. Resistivity. We can get the high power factor as a square sigma. So that's the three. Things separately. But with increasingly. A stringent. Realizing, condition. So here is our recent, experiment, to work, showing. These predictions. So the first. This is, a transverse. Thermal electrical. Conductivity. So that's actually a combination, of the four, independent. Parameters. Like uh, as xx. Rho yx. As yx and the row xx. The longitudinal. Transverse. Electrical, resistivity. And. Thermal power. And the first thing we show that. It reaches the unit, this unified. Universal. Constant. When we apply high magnetic, field, and agreed, quantitatively. With the theoretical. Predictions. Because as we imagine. All these parameters. Like longitudinal. Resistivity. Is certainly, highly dependent, on temperature. On magnetic, field, and even material, specifics. And here, after the combination, of four, independent, parameters. The final number becomes the independence. Of anything, on the material, specifics. Only highlights, the contribution. From the topological. Singularity. Making it a universal. Constant. And the second, thing is more related, to this longitudinal. Thermal power. As we can see so this line is some ideal, gas. Entropy, can be reached. And. If we have this. Very, low. Transverse, electrical, resistivity. And we can show that. Really, increase. This value, of this longitudinal. Thermal power which. Very high. This value, and also at the low temperature. So the difficulty, for low temperature, can be understood. Because. Many thermal electrics. Working, at a high temperature. Far above room temperature. Because, that's good to, increase, the entropy. But here the peak value is about like a 50, kelvin. So the, internal, materials, the entropy, are very low, but still can reach very high. With a thermal power like an older magnet, higher than the ideal gas limit. And to see that this is indeed the case dominated, by this quantized. Thermoelectrical. Hall, so just can decompose. This longitudinal. Thermal power, into the two contributions. And we can see. This transverse. Part of the thermoelectric. Hall, can dominate. This whole 90 percent, of the longitudinal. Thermal power. So the, last thing, we like to, show, is more related, to, this power factor. So the power factor, is this like as square sigma or as a square row, to be more precise. Using a tensor. Language. To to give a comparison. So this top row is an example, on the, another, top topologically. Trivial. Semi-metal. Like a bismuth. And it has like a power factor. About five. And for this one semi-metal. Is about like a 500. So that's, also like 10 times. Higher. Than the, best, like thermal electrics. Like uh leather telluride. Business, telluride. Now those materials, they reach very high. This power factor, at elevated, temperatures. And, it's also 100. Times higher, than the similar, type of the semi-metal. Materials. So at this stage, and we can think, that we can truly utilize. This topological, singularities. As a source. To harvest. Energy. As a brief. Summary. So today we provided, two examples. On using. A topological. Singularities. And the first to induce. This kong anomaly, which is we can see, electronic. Topology. Using the lattice, degree of freedom, with a few normal features. Like the chirality, selection. Between the singularities. And the phonon, energy of, the dynamical. Effects. And also a parallel, divergence. So this one limited, by the instrument. We cannot, confirm, or deny, this stage. And then the other more practical, energy application. Is we can use that to generate. A giant, thermoelectric. Response. One thing is related, to the, more. Quantized. Thermoelectric. Hall conductivity. Even the materials. Resistivity. Thermal power, they are all highly dependent, on materials. Temperature, magnetic, field, and the combination.
Is Really a very simple. This universal. Number here, and there is also, large. Linear. Proportional, to magnetic, field, not such a reading thermal power here, and finally. And, just, using the singularity. We can also generate. A high, thermal powers, with order of magnitude, higher. Than reporting, materials. So with that. I will just stop here. And, acknowledge, my. Group members. And all the collaborators. And the department of energy for the support. So with that thank you for your attention. And happy to take any questions. Well thank you professor, lee. I'd like to just take a few minutes to, remind, alumni, and anybody else who, uh is watching today that you can ask questions, by using the q a feature in zoom. And you can also, upvote, questions that have already been posed so. Let's give people just a few seconds to type their questions in and. Upvote anything that they're particularly interested in hearing. About. All right so um, i'm seeing some upvotes for a question about any sustainability. Implications, of this. Work. Professor, lee is that something you're able to address. Um. Yes. So. Many questions. There are some earlier, questions, so we start from, there. But i was going by the uh the number of uh, votes that a question had received. Um. But uh. We can we'll start with one um. From the very beginning then we'll jump to the most popular one and sort of go back and forth okay the first question was about um. A project, developed by, bill gates that was addressed, in his, netflix documentary. Uh regarding, small nuclear plants. Being used in radioactive, fuel. Is this something. That you think is feasible. Um, and is there. Any reason why the u.s, shouldn't be promoting this. Um. I don't know if you're able to draw any connections, between that question, uh and your talk, um. Yes, i think that's actually, a, great question, and there are also. A, deep connection. Between the like nic, and their alumni. And working with like very small. Reactors, and even, and this, next generation, reactors. I i'm not certainly, expert, in working with a, physical reactor. But. There are certainly, many. Treatable, components. There. And to, promote, it and i believe that's also maybe biogas. May have some confidence, that may work out, and with very good permitting, results. And, for the, uh this us why not promote that i think that's a. Uh. Many practical. Issues, here like the, regulation. And other things, but when the time, is good i'm pretty sure there are still, many exciting opportunities. In the next generation, reactors. And i still feel optimistic, in that area. No. Thank you uh for that answer, um. Let you go back to uh the question, which was. Still the most popular, one um i think people are interested in hearing about the sustainability. Implications. Of your work. Yes, so, some of the electrics, have been. Very brought up for, almost like uh 50 years. And, compared, to other, this energy. Harvest, measure, like the solar panels, it has been. Less implemented. The one major, reason, is the, lct. All this efficient, is not high enough. And here. What we will say. If we can really, find a highly distinct. Mechanism. That can, break the barrier, and truly make use, of thermal electrics. As a source of the energy. It can actually harvest, many, uh like a waste of heat not necessarily, using. Um. Like a, sun, and it can be used like even some, waste heat in our home heating system, or in our body heat, so many of these kind of waste of heat.
They Composed, of like a, 60, 70, or even higher percent. As rejected, heat you know currently. The u.s, energy structure. And imagine, if we can use, those amount of waste heat to do, energy conversion, so that will be the main. Driving force, to support, sustainability. Hope that answers your question. If people, follow on questions please feel free to type them up into the q a feature and we can continue, with particular, threads if there's a lot of interest. Next question. These questions, are very broad in range, which makes this fun. Some people are wondering. It says, some folks have two worlds on their hair how do you explain. Two local, topological. Singularities. Yes that's a great pattern, let me. Show you from the. From from the pollination. In that page. So some people can even have three but more likely. There are two will cancel out as one positive, chirology, and one negative, priority. And here you can see uh use the term approximately. The reason is that uh the human hair is not of a full, clothes the sphere, but more or less, kind of severe. So that means, we can really actually, push another singularity. Into. Into the sphere but with the overall. The energy, like a higher. So that's, that's the case so it not becomes, so mathematically. Rigorous, it's not a really. Uh like ideal, severe in that case. Thank, you, um. Another question, uh, jumping topics again how difficult, or expensive, is it to manufacture, these wild semi-metals, at volume. That's a, wonderful, question, so. At our. Lab scale. I would say this, for the fundamental, measurements. The cost, is not a concern. So i think we are still at. Haven't reached that stage, we still want to get a higher quality, crystal. And. Get to make it measurable. And like a high precision, thermal measurements, we really needed to have, a high quality, large a single crystal, to even carry out this type of measurements. The brief answer. Because this. Cost is high, and, but we would think if there are some. Highly plummeting, materials. You know gradually. It will come to the stage, uh for the massive production, there are still a few different hurdles. To overcome. In order to, to achieve that. So right now it's far from. That scale. Okay. Um, can you talk about the uh the range of temperatures. Over which, um. These materials, are likely to be useful. Yes, so, that's a great question. For this particular, materials. And if it's below, like a. Nitrogen, temperature. So you can imagine, if we want to. Do something at a cryogenic. Temperature, we use the liquid of helium, at the four kelvin, equator, nitrogen. 7k7. Kelvin. But the thermal electrics, if we run it backward. Which means that we inject the current, and can make it according as the peltier. Effect. And we can actually, do cryogenics. And without, using, nitrogen, or heating. So if we have some material, with. High performance. Near heating temperature. We can make a refrigerator. And currently. People are using like a healing three theme for, like a that kind of dilution, to. A fridge, and then we can use some like a, cryogenic. Free. Fridge, by using, thermoelectrics. So that is one major application. But the other, major application, is certainly. Uh, to push it into roon temperature, range. And that's. As long as the materials. Let's say the materials, by material we mean it has a brilliant. Momentum, space, and all these singularities. They are fixed. Then the working temperature, is almost. Fixed, so imagine if. One day some people design, a real, very optimized, material, just for room temperature. That can also be. Permitting. And to make the working range, accumulable. But not in this state. We've got. Another question, uh why would one prefer, energy harvest, from thermoelectrics. Over methods like heating steam and running a turbine. That's a great question, so. Heating is actually, the reason, it is just, the answer. So, the, heating, steam or the, turbine they have moving parts, so one reason people, promote, the thermoelectrics. Is that, it only needs a fixed, synthetic. Part, of semiconductors. Without, you having any moving parts. And the other is also, the heating steam the turbine they really are harvesting, from high quality, heat. And, we don't want to do turbine in our body. And, even some like international. The internet of things. And the very, this is a tiny, amount of the waste heat, generated. From our daily. This. Equipment. From our body temperature. Those kind of heat, can also be harvested. Using this small device, of the thermoelectrics. That's another, application. Area, not possible for the, turbines. We've got a question, now. About the people doing this work, can you talk about your grad students and how they're doing, um, and. People are also curious who your biggest competition, is for grad student, talent.
And. Yes. Well i think, overall, this works. Done and led by graduate students. And. We don't have many well in if we're talking about my own research, group we have, four graduate students, ones not listed, here, i think they are doing great, and. I'm really i feel very lucky having them working together with me on, all these, topics. Um. Can you comment a bit on who your biggest competitors, are or is that a trade secret. Competitors. I would say. There are, few groups we have to, share the goal, and try to achieve the same thing sometimes, they reach from. Some, computation. But overall, review. Is all more like also a constructive. Computation. Some other group they tested the new phenomena, in a different, uh materials. Like uh, there's a quantized, thermoelectric. Hall another group they, tested. In dirac, semi-metal. And we do wild semi-metal. So that's sort of a competition, but i feel we both. Contributed. Constructively. To confirm. Some normal mechanism, going on in these types of like a single languages. So not so worried. Okay, thank you. Um we have a comment from, david quinn david, are you still online. Here. If you are and you wanted to make your comment live, um, please feel free to do so. Um. David had a. A comment about waste heat application. And how it would probably work very well for, combined, cycle, gas turbines, um i mean i don't know if you want to. Comment on that, i think that's certainly very true, and, this waste of heat in gas turbine, is working, already. Very kind of mature, and. Going on extremely, well. And, so that's a i really don't think that's the field, for, thermal electrics, working, at that. Kind of environment. I'm still thinking, as a different, application, scope, like in my office. We have like a heating system. Very small things or even like uh, this is we have a like a computer, that kind of very low grid. Uh waste heat so that's a kind of waste heat is. Which much lower quality, than the waste heat, in gas turbine, and also much lower. The temperature. Gap but still, there's some chance to generate, electricity. From there, so. But i would say, yes there's a, very. Promising, this going on in class turbine. Thank you um, david if you had any, other comments, um. Please chime in. Um. I'll go on to the next question what predictions, do you have for quantum, computers, being. 100. Fault tolerant, and being mass-produced. Uh-huh. Yes that's, an awesome question. I think, just, like the, classical. Computers. There's also. This area, and thoughts, on quantum computing. There are there are two things at least, going on. One is topological. Quantum computing. So that used like uh some, local. Uh this uh states. And so destroy, one it won't destroy, the other, that. Provides, some like a, layer of topological. Protection. To to make it like a force of tolerance. But the other thing is just like a classical, computer. There's also some post, processing, like the error correcting, codes. And algorithms. And there are i'm sure there's, active. Research. In a topology, in the quantum computing, they also design this kind of. Phospho-tolerant. Algorithms. And so it doesn't have to be, 100, percent, error tolerance, just to buy the, materials. Itself, they can even correct. Afterwards. Um, last question here, if anybody else has any other, questions i'd encourage you to type them into the q a function. Are there, applications. For. Heat pumps heating and cooling in conjunction, with electrical, production. And. So, i'm not entirely, following the pattern you were talking about. Thermal, it sounds like a more or less, like a thermal, thermoelectrics. There is a heat source there is a heat sink, there is a temperature. Difference, between that two parts. And, we can produce, electricity. From there so that's the, essence, for thermal electrics. So, that might be. The. The answer, to this but maybe, the audience have a specific. Configuration. In this. Stage. Thank you professor, lee um that was a very informative, talk and you certainly answered. A range of questions. Um. I'd like to thank you for your time, and on behalf of the alumni association. Thank you everyone for tuning in to the mit, faculty forum online, today. Um. We'll be keeping, uh. The q a up for another 15 minutes or so if anybody, wants to uh. Actually, sorry. An additional question just popped up um going back to the question around. Temperature range, is there any chance we could find thermoelectrics. That work at or below. The hg4, boiling, point. Actually, a brief answer is yes. There are. Some other materials, people have been studied. Some. Kind of, weird, ion based, compounds, and they actually work at a very, low temperature. And with a very different, working mechanism, with like a wild shiny metal. But it certainly, is impossible.
Okay. Well thank you for, addressing, that, last question. As i was saying we'll keep the chat window open, for another 15 minutes or so if anyone, wants to network, this broadcast will be available, on the mit alumni association, youtube channel, within a week of today's, airing, once again, thank you for watching, and we hope to see you again on a future broadcast. Thank you everyone. Thank you. Thanks for joining us and for more information, on how to connect with the mit alumni association. Please visit our. Website. You.
2020-11-13 11:12